2. 山西冶金岩土工程勘察有限公司, 山西 太原 030000
2. Shanxi Metallurgical Corporation Geotechnical Engineering Investigation, Taiyuan, Shanxi 030000, China
地质灾害是一种危险性极大的地质现象,多由地质条件变化、极端天气、人为扰动等原因引发,呈隐患多,分布广,易突发的特点,严重损害人类生命财产安全,极大制约中国的可持续发展战略。近年来,中国多省地经济快速发展的同时地质灾害发生频率也随之升高,山西省尤为突出。2023年7月,山西省政府出台了该年度地质灾害防治方案,晋西黄土高原部分地区离石、石楼、柳林三地因植被覆盖减弱,用地类型改变,建筑兴起,交通网络日渐密集导致灾害频发被划定为重点防治区。
地质灾害发生态势多不可控,且易对生态、基础设施、人员造成严重损害[1],提前预测灾害高发范围对于精准划定防治区域、早期救援以及居民安全规划至关重要[2]。区域地质灾害易发性评价是通过分析孕灾因子与灾害点的关系继而确定灾害易发的最佳组合[3],并将特定区域内的地质灾害发生空间范围可视化。该方法可为区域地质灾害预防与治理工作提供参考,有效减少伤亡。
近年来,在GIS技术支持下,地质灾害易发性评价方式不断改进,理论体系日趋完善,最初的定性分析逐步发展为客观性更强的定量分析[4]。基于专家经验的定性分析方法(层次分析法(AHP)[5])客观性较差,易受主观因素影响[6]。定量分析可分为机器学习、统计方法两大类。人工神经网络(ANN)[7]、随机森林(FR)[8]、深度学习(DL)[9]、逻辑回归(LR) [10]等机器学习方法,大多需要频繁迭代运算、调整参数,操作相对复杂[11]。统计分析法因其操作简便备受研究者青睐,应用相对广泛[12],诸如信息量法(IM)[13]、确定性系数法(CF)[14]、证据权模型(WOE)等[15]。提高统计方法精度是国内外学者近年不断研究的热点之一。梁丽萍等[16]采用信息量与确定性系数相耦合的方法探究四川省泸定县地质灾害易发性;陈飞等[17]以信息量为基础,结合神经网络模型对评价结果进一步训练以预测江西上犹县滑坡发生概率;Devkota K.C.等[18]采用逻辑回归及多种统计方法对喜马拉雅山区展开滑坡易发性评价,经过对比分析寻找研究区最优模型。Shano L.等[19]采用多种双变量、多变量等统计法展开研究,得出不同区域应根据其调查目的、地质条件等采用不同方法的结论。
本文结合研究区地质灾害发生特征,以统计方法为基础,同时耦合地理探测器,分别结合IIM,IM,CF建立评价模型,对研究区地质灾害易发性展开分析。
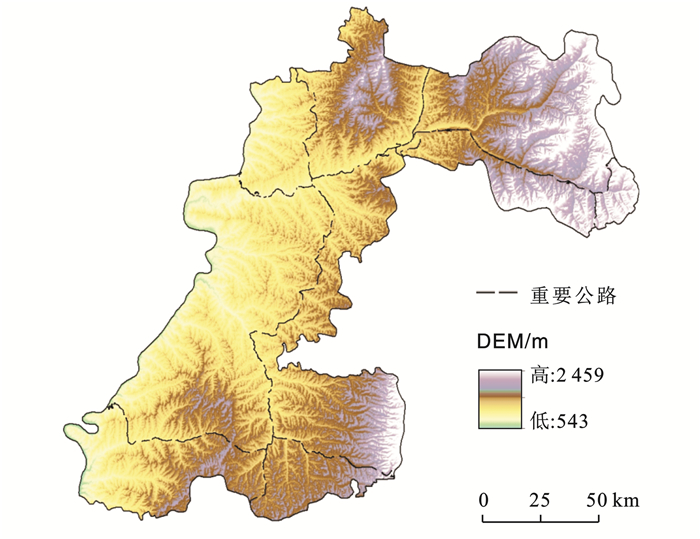
1 研究区概况山西省吕梁市中南部离石、石楼、柳林三县(区),是华北地区通往大西北的重要中枢,位于黄河东岸,吕梁山西麓,地跨北纬36°51′—37°42′,东经110°28′—111°35′,属晋西黄土高原的一部分,是山西省受地灾影响最为严重的地区之一(图 1)。地貌形态主要为中山、丘陵两类,地形起伏大,海拔在900~1 600 m之间,陡坡深沟交错,多被厚层黄土覆盖,植被生长不均衡,年降雨量460~561 mm。区域内断裂构造不发达,离石大断裂为主要断裂带,北起离石,南至石楼,压性结构面特征突出,断裂面近直立或向西倾,断距较大;地层发育较为完整,除古生界奥陶系上统、泥盆系、志留系、白垩系上统有缺失外,其余地层均有出露;近年来经济发展较快,道路繁复,青银高速、沿黄旅游公路等交错纵横。
|
图 1 研究区地形 Figure 1 Toporaghic map of study area |
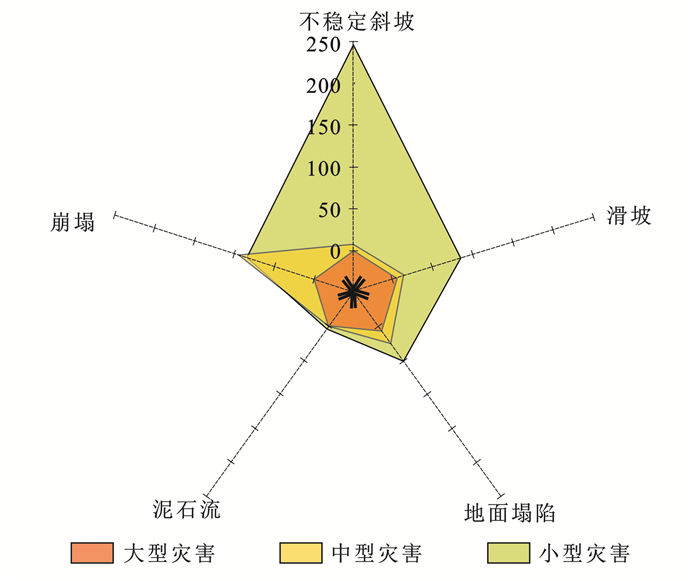
截至2022年底,研究区共累计发生525处地质灾害,不稳定斜坡、滑坡、崩塌为主要地质灾害形式(图 2)。2018年4月30日,离石区枣林乡彩家庄遭遇滑坡事故,被埋9人全部遇难[20];2021年10月5日,石楼县发生黄土崩塌,致1人遇难。地质灾害的频发对当地人民生命和社会经济造成了严重损害,已成为制约该地区发展的主要因素[21],因此,亟需研究精准预测该区域地质灾害易发性的方法。
|
图 2 研究区地质灾害类型及程度 Figure 2 Types and degrees of geological hazards at study area |
DEM数据采用Earthdate 2020年2月18日最新出台的NASA DEM V001 dem数据,空间分辨率30 m;土地利用数据由地理空间数据云网站获取Landsat 8 OLI_TIRS卫星影像,应用ENVI软件进行裁剪、辐射定标等预处理,选取特征数据进行监督分类,目视解译而来,空间分辨率30 m;地貌类型由中国1∶100万地貌图提取而来;土壤性质来自ISRIC-World Soil Infotmation;植被覆盖度由NASA官网提供的MODIS数据采用MODIS Reprojection Tool软件提取而来;岩性、断层数据源于中国地质调查局地质云提供的1∶50万基础地质图;河流及道路数据由全国地理信息资源目录服务系统获取;坡度、坡向、曲率、地形起伏度数据由DEM借助ArcGIS 10.2提取得来;30 m分辨率多年降雨数据由中国科学院成都山地灾害与环境研究所数字山地与遥感应用中心提供;地质灾害空间分布数据由中国科学院资源环境科学与数据中心获取,经Google遥感影像进行目视检验并通过实地考察进行验证。
2.2 研究方法 2.2.1 信息量模型1948年信息论创始人Shannon提出信息量法[22],后逐步发展到地质行业灾害预测领域。其核心思想是通过计算各指标因子不同的分级状态对灾害发生所贡献的信息量来表示其对灾害的孕育程度,并对灾害易发性等级进行划分。公式为:
| $ I_{i j}=\ln \frac{N_{i j}-N}{S_{i j}-S} $ | (1) |
式中:Iij为指标因子xi划分区间j对地质灾害事件提供的信息量;Nij,Sij为因子xij区域内的灾害点数量及xij的区域面积;N为区域内灾害点总量;S为区域栅格总面积。
由公式可知,Iij越大,灾害点提供的信息量越大,因子xij对地质灾害发育影响越大,地质灾害越易发生。由此,依据信息量原理,提出可以增加考虑非灾害点所贡献的信息量,补充利用随机分布的非灾害点进行上述因子分级信息量计算,用Ⅱij为代表,以表示各影响因子不同分级状态对灾害不发生所贡献的信息量,即Ⅱij越大,地灾不发生的可能性越大。
| $ \mathrm{II}_{i j}=\ln \frac{M_{i j}-M}{S_{i j}-S} $ | (2) |
式中:Ⅱij为xij因子对地质灾害不发生所提供的信息量; Mij,M为xi影响因子j分级区间内的非灾害点数量及研究区非灾害点总量; Sij及S仍为xij区间所占栅格面积与区域栅格总面积。
考虑以上各点提供信息量,以评价单元中灾害点提供信息量与非灾害点所贡献的信息量之差表示改进信息量:
| $ H_{i j}=I_{i j}-\mathrm{II}_{i j} $ | (3) |
式中:Hij为考虑非灾点后的xi指标因子的j分级状态所提供的综合信息量。Hij越大,相应评价单元地灾发生的可能性越大,灾害易发性等级也越高。
2.2.2 确定性系数法确定性系数法是概率统计方法的一种,假定历史灾害点地质环境等条件不变,计算各分级状态下灾害发生的相对概率[23]。用CF表示,值域为[-1, 1], 大于0表示地质灾害发生确定性较高; 小于0表示有较低确定性地质灾害会发生; 越趋近-1越不易发生地质灾害; CF=0表示不能确定地质灾害是否会发生。公式为:
| $ \mathrm{CF}= \begin{cases}\frac{\mathrm{PP}_a-\mathrm{PP}_s}{\mathrm{PP}_s\left(1-\mathrm{PP}_a\right)} & \left(\mathrm{PP}_a<\mathrm{PP}_s\right) \\ \frac{\mathrm{PP}_a-\mathrm{PP}_s}{\mathrm{PP}_a\left(1-\mathrm{PP}_s\right)} & \left(\mathrm{PP}_a \geqslant \mathrm{PP}_s\right)\end{cases} $ | (4) |
式中:PPa表示a分级区间内灾害点数量与区间面积的比值; PPs为研究区灾害点总量与研究区总面积的比值。
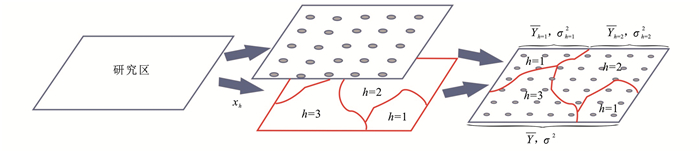
2.2.3 地理探测器地理探测器是一种基于空间分布异质性(图 3)[23]与方差理论以q值为度量的处理多类型变量的空间分析方法[24],也是目前学者研究驱动力及因子分析的工具之一。其核心思路是:假使某自变量X对因变量Y有重要影响,那么两者应具有相同的空间分布。q值计算见式(9)。
| $ q=1-\frac{\sum\limits_{h=1}^L N_h \sigma_h^2}{N \sigma^2}=1-\frac{\mathrm{SSW}}{\mathrm{SST}} $ | (5) |
| $ \mathrm{SSW}=\sum\limits_{h=1}^L N_h \sigma_h^2 $ | (6) |
| $ \mathrm{SST}=N \sigma^2 $ | (7) |
|
图 3 空间分异性原理 Figure 3 Principle of spatial heterogeneity |
式中:Nh为区域h的单元数; σh2表示Y值方差; N和σ2为研究区总单元数和Y值方差。SSW及SST为各区域方差之和及研究区总方差[25]。q值表征各个影响因子的贡献率, 值域为[0, 1], 越接近1说明Y的空间差异越显著。本文利用归一化后的q值作为各因子的一级指标权重以量化因子间差异性。
2.2.4 相关性检验评价因子的选择在地质灾害易发性评价中起着关键作用,直接影响模型的最终精度。本文利用Python语言计算两两因子间相关系数以排除存在相关性较大的因子,避免其对模型结果造成影响。
19世纪80年代,卡尔·皮尔逊等人提出皮尔逊相关系数(Pearson correlation coefficient),该系数适用于衡量呈正态分布的连续变量间的相关程度,是目前统计学中计算相关性的有效方法之一。设(X, Y)为二维连续变量,相关系数表达式为:
| $ \rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_X \sigma_Y}=\frac{E〔(X-E X)(Y-E Y)〕}{\sigma_X \sigma_Y} $ | (8) |
式中:ρ表示相关系数; cov为协方差; E为数学期望或均值。
ρ范围在-1~1之间, 0表示没有相关性, 接近-1或1则表示两因子呈负相关或正相关关系。
2.3 模型验证 2.3.1 SCAI种子验证法种子细胞面积指数(SCAI)于2004年提出,由Süzen等[26]给出公式,后多应用于验证评估模型的准确性,应用于地灾易发性评价体系中,SCAI可定量表示各级别与灾害发生的相关性,表达为:每一易发性级别的面积百分比与每个级别的地质灾害百分比的比率。SCAI越低表示地质灾害易发性水平越高,模型精度越高。在高易发水平下具有SCAI值较小,低易发性水平SCAI值较大即表示模型分区合理准确。
2.3.2 ROC曲线受试者工作特征曲线(ROC)反映了数据特异性和敏感性的持续变化,早年应用于医学行业,后国内外学者逐步应用到灾害评价领域。其横坐标由正确预测非灾害点的比例(1-特异度)构成,纵坐标为正确预测灾害点的比例(灵敏度)组成[27]。
在易发性评价模型验证中,ROC曲线可以看作分类器对模型分类效果的评定,由其线下面积AUC值作为度量指标,值域为[0.5, 1]。曲线能够简单直观地反映出所选方法和易发性结果之间的关系,准确性较高。AUC越接近1说明模型预测结果精确度越高[28]。
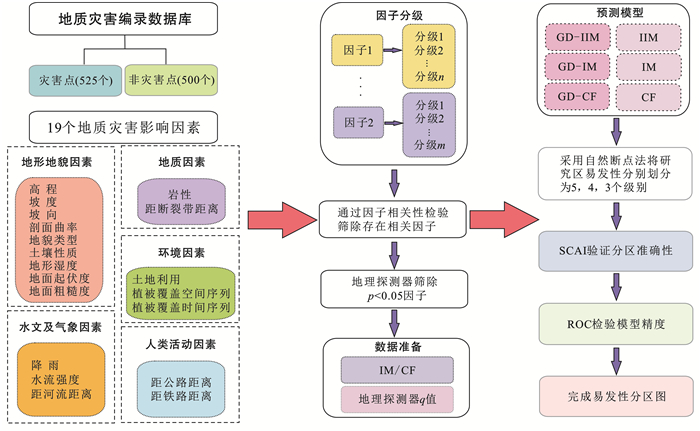
2.4 研究区模型构建为使得非灾害点能尽可能多地表达出不利于地质灾害发生的因子特性,利用ArcGIS 10.2软件在距灾害点2 500 m缓冲区外随机选择500个非灾害点与之混合,并以8∶2比例进行分配,最终得到由820个样本点组成的训练集以及205个样本点组成的验证集。
首先,对各影响因素进行分级,用以地理探测器因子探测。对于显著性较差(p>0.05)的孕灾因素予以剔除。其次,结合因子重要性,通过相关性检验筛除与多数因子相关性较大的影响因素,最终确定12个地灾指标因子。从训练集出发,以探测器q值表示各灾害指标因子对地质灾害发生的影响程度,分别耦合IIM,IM,CF构建加权模型,以SCAI,ROC曲线对结果进行验证(图 4)。加权公式为:
| $ \mathrm{LSI}=W_1 X_1+W_2 X_2+\cdots+W_o X_o $ | (9) |
|
图 4 地质灾害易发分区定量分析流程图 Figure 4 Process diagram for quantitative analysis of geo-hazards susceptibility zonation |
式中:LSI为地质灾害易发性综合指数; Xo(o=1, 2…12)为o因子;Wo表示评价因子o对应的归一化后q值。
3 研究区地质灾害易发性评价本研究遵循地质灾害评价流程,主要依托ArcGIS 10.2平台展开:首先,对影响因素进行筛选,以避免因子间相关性及因子冗余对结果造成影响;其次,用训练集构建6大预测模型并结合测试集展开模型精度验证,选取适宜于本研究区的最优模型;最后,将评价结果分级制图,直观呈现灾害易发性分布情况。
3.1 评价因子的确定地质灾害成因复杂,由多种因素共同决定。评价因子的选取对地质灾害易发性评价至关重要[29],构成了其空间预测的不确定性。
3.1.1 因子初选及预处理研究区多为黄土覆盖,植被覆盖变化分明,海拔特征明显,由中山区、丘陵区相交而成。2022年山西省政府亦发文指出地灾重点防治区应着重排查公共道路地区以降低灾害隐患。故本文结合研究区地理条件、数据可获取性、政府公告以及研究地区地质灾害高发类型(不稳定斜坡、滑坡、崩塌)孕灾条件,从地形地貌、基础地质、水文气象、环境、人类活动方面共收集了19个相关因素,以30 m*30 m栅格为划分单元将全区共划分为4 817 414个评价单元。
为进一步对地质灾害易发性展开评价,将各影响因素进行预处理及分类操作。离散型数据按属性分类,连续型数据中将影响范围有限的因素如“距河流距离”等以等距法分类,其余均采用自然断点法分类。
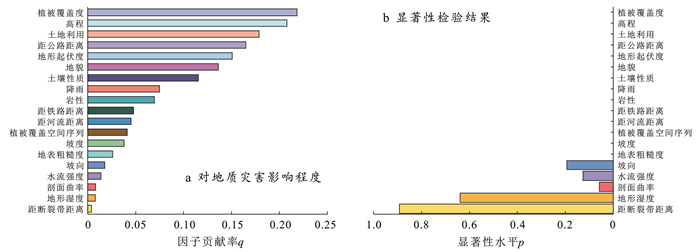
3.1.2 评价因子检验及确定赋值灾害点为1,非灾害点为0,利用地理探测器对各影响因素进行因子探测同时筛除不显著因子,探测结果(图 5)。
|
图 5 地理探测器地质灾害因子探测结果 Figure 5 Geo-hazard factor detector results of geographical detector at study area |
各因素对应q值表示其对地质灾害的影响程度,用于耦合IIM,IM,CF构建易发性评价模型;p值表示相应因子的显著性检验结果,通常以0.05为界,小于0.05表示差异显著,大于0.05表达为该因素对地质灾害发生影响不能确定,值越大说明该类型变量对灾害发生有影响这一推断的可靠性越低,故将其对应因素剔除。
由图 5b可知,坡向、地形湿地,水流强度、剖面曲率、距断裂带距离5个因素p值均大于0.05,显著差异性过小,予以剔除。
为避免因子冗余及相关性对统计结果产生影响,利用Python语言对剩余得到的14个因素进行相关性检验(见图 6),以剔除各相关较大因子。
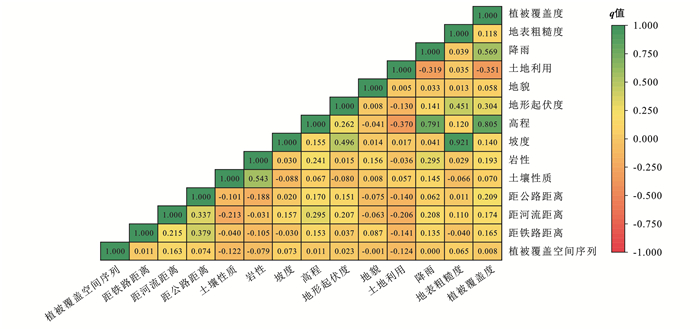
|
图 6 研究区各地质灾害因子相关性热力图 Figure 6 Factor-related heat map of geo-hazard at study area |
如图 6所示,高程与降雨、植被覆盖度存在较大相关性;坡度与地表粗糙度相关系数高达0.921,以尽可能少地剔除因子为原则,结合地理探测器q值结果,决定删除高程、地表粗糙度两因子。最终选定:NDVI值、土地利用、距公路距离、地表起伏度、距河流距离、土壤性质、坡度、降雨、岩性、植被覆盖空间序列、地貌、距铁路距离共12因子作为灾害易发性评价指标(图 7)。

|
图 7 研究区地质灾害影响因素空间分布 Figure 7 Spatial distribution pattern of impact factors on geo-hazards at study area |
依据筛选结果及评价指标等级划分,统计各因子二级状态下的灾害点、非灾害点数量及栅格面积,利用IM模型下的公式(1),(2),(3)分别计算每个一级指标下的各二级指标权重(表 1)。
|
|
表 1 研究区各地质灾害评价指标统计值 Table 1 Statistical values of each evaluation index of geo-hazard at study area |
将GD-IIM,GD-IM以及GD-CF三模型相应地质灾害易发性图与选定的12因子图叠加,分析不同因子与易发性水平的关系。不同地灾易发程度下,各因子面积百分比见图 8。下文对本研究区影响灾害发生最大的4个因子展开描述。
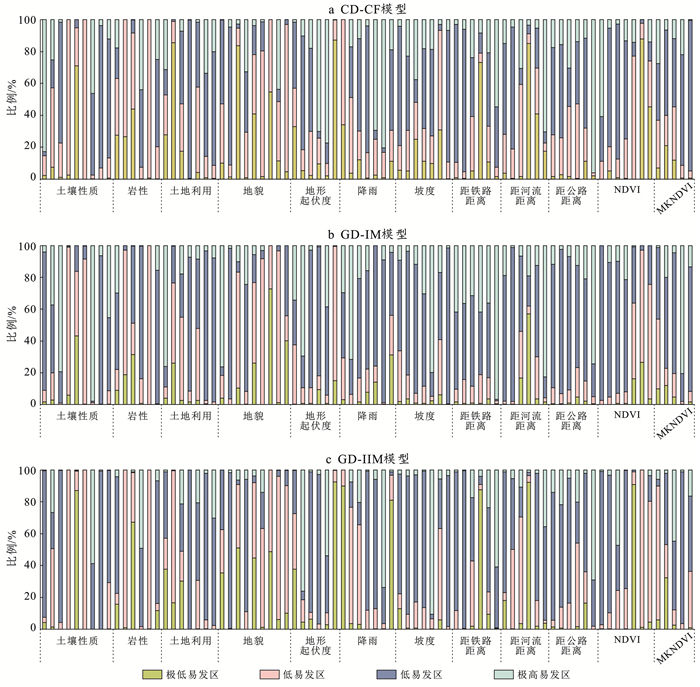
|
图 8 研究区不同地质灾害易发性等级下各因子所占百分比 Figure 8 Percentage of each factor at different susceptibility levels of geo-hazard at study area |
由因子探测结果可知,NDVI是决定本研究区地质灾害易发性的重要因素。植被可以加大地表粗糙度,同时对雨水有一定遮挡能力,可以起到降低入渗量的作用;同时,植被根系可以保持水土稳定,提高土体的抗冲、抗蚀强度。所以,一般情况下,NDVI值越高,越能防止浅层滑坡、不稳定斜坡等地质灾害的发生。
不合理的土地利用方式是地质灾害现象加剧的重要原因。由图 8可知,研究区建筑用地、水域、耕地3种地类地质灾害点密度较大,易发性均呈高、极高状态。原因在于这3种地类周围人口密度较大,人类活动多,易造成山地植被破坏,降低了土层稳定性,同时,各类水资源容易渗入基底软弱地层,孔隙水压力增大,易形成滑动面,从而引发滑坡等灾害活动;灌木林地面积较小,加之树木根系发达起到固土抗滑作用,并能截流抗蚀,为地质灾害提供不了物质基础,故基本处在低易发或极低易发区域;裸土地表层无植被覆盖,土壤肥力衰退,面积比例最小,研究区大部分范围被草地、林地覆盖,故而4种易发性区域均有涉及。
近年来,人类工程扰动对地质灾害影响愈发剧烈,受到多地政府的重视。通常情况下,山区地形条件复杂,地质环境脆弱。然而,交通公路的建设导致切坡、填沟、爆破等操作不可避免,加剧了土壤松动,严重破坏了地质环境,极易诱发不稳定斜坡、滑坡、崩塌、地裂缝现象。由图 8可知,与公路距离较近时,高易发、极高易发区面积比例增大,随着与公路距离的增大,地灾活动也逐渐减少。当超过2 500 m范围时,高易发及以上区域面积比例减少,原因在于距公路超过2 500 m范围面积较大,灾害发生密度相对降低,故而极低、低发区面积占比有所回升。
地形起伏度为一定区域内最高点与最低点的高程之差,是描述地貌形态的重要参数,也是斜坡稳定性的表达要素。地势平坦,地貌形态单一地带因其剪应力也相对较小,发生地质灾害的概率同样很小。随着起伏度的增加,产生滑动的剪应力也不断增加,地质构造越发活跃,发生滑坡灾害的概率也随之增大。
4.2 模型验证 4.2.1 SCAI对GD-IIM,GD-IM,GD-CF三模型的分区情况展开验证,以确保研究区地灾易发性评价分区准确性。为得到最可靠的划分级别,采用自然断点法将研究区分别划分为5,4,3个易发性等级,并分别进行SCAI检验,最终确定合适易发性等级。结合ArcGIS 10.2区域统计工具,将灾害点与评价结果叠加,计算不同等级下灾害点个数、分区面积及相应SCAI值。
由SCAI验证原则可知,构建模型需满足易发性等级与SCAI呈反向相关关系,即当各易发性区间的SCAI值随易发性级别的增高而降低时说明地质灾害发生情况与易发性分区一致,区域划分准确。
为在图中直观表示SCAI变化情况,将个别过大数据进行了倍数缩小处理,横坐标以数字表示易发性等级的升高(图 9)。
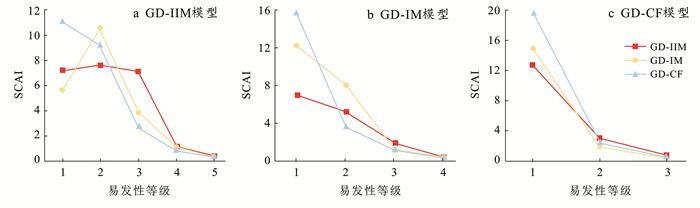
|
图 9 GD-IIM,GD-IM及GD-CF模型在研究区不同地质灾害易发性分级区间下的SCAI值 Figure 9 SCAI verification results under different geological hazard susceptibility intervals of study area by three models |
图 9a中,GD-IIM,GD-IM的极低易发区与低易发区SCAI呈上升态势,易发性水平越高,SCAI值反而越大,分级不合理。图 9b,9c中,模型被分为3个易发区及4个易发区时,SCAI值均满足随易发性等级升高而降低的特征。相较于3个易发级别,当研究区被划分为极低易发区、低易发区、高易发区、极高易发区4个等级时,分区内容更为细致、有效。且GD-IIM,GD-IM,GD-CF最高易发区SCAI值分别为0.399,0.464,0.362相较划分为3级别下的最高易发区0.495,0.824,0.52的SCAI值数值更小,说明划分为4个级别下易发性模型的预测错误率可得到更好的控制。得到最终地质灾害易发性分区图(图 10)。

|
图 10 各模型地质灾害易发性评价图 Figure 10 Evaluation of the susceptibility of geological disasters in each model |
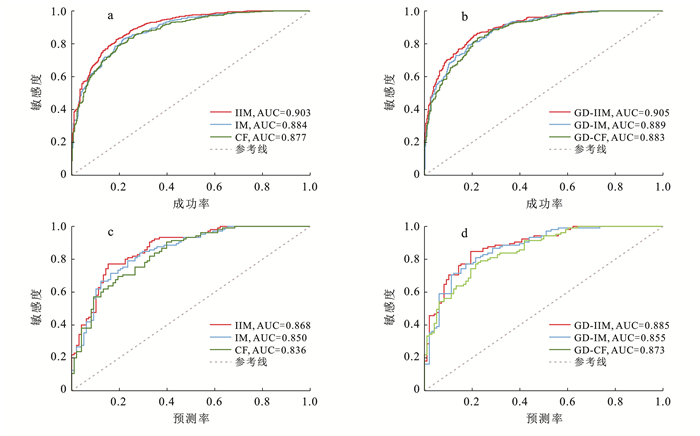
经ROC检验,由图 11a,11b训练集构建的成功率曲线所示IM,IIM模型AUC值分别为0.884,0.903;GD-IM,GD-IIM对应AUC值为0.889,0.905;图 10c,10d中,测试集构建的预测率曲线下IIM,IM模型AUC值分别为0.868及0.850,GD-IIM比GD-IM模型AUC提升3%,由此可知,无论是成功率还是预测率,考虑非灾害点信息量模型相较均表现出较好结果。
|
图 11 各模型的成功率和预测率的ROC曲线 Figure 11 ROC curves of success rate and prediction rate for each model |
易发性评价模型对于地质灾害防治具有重要意义。为提升统计模型结果精度,优选出最适宜本研究区的灾害评价模型,本文将地理探测器的因子探测结果作为因子权重,耦合各类统计方法,并从传统信息量模型出发,考虑灾害点信息量的同时综合考虑各指标因子不同分级状态下非灾害点所提供信息量,以此提高最终模型结果精度。视归一化后的地理探测器空间分异性q值为权重分别与IIM,IM,CF相耦合构建研究区6大地质灾害易发性评价体系,按照8∶2比例将样本点划分为训练集和测试集。
由于易发性分区准确性与区划数量及方式密不可分,本文采用自然断点法分别将研究区易发性级别划分为5,4,3个等级,利用SCAI验证分区准确性从而确定最合理的分划等级,并以ROC曲线对各模型结果进行精度评价。
得出结果:各模型划分为极低、低、高、极高4个易发性区域时SCAI值与易发性等级呈负相关,且分级效果良好,最为合理准确,满足要求;基于GD-IIM,GD-IM,GD-CF模型的预测率曲线AUC值分别为0.885,0.855,0.873,表明应用双变量统计法耦合地理探测器模型预测效果较好,适宜应用于本研究区易发性评价模型构建;结合成功率曲线、预测率曲线结果及极高易发区SCAI值(GD-IIM,GD-IM模型SCAI为0.036,0.045)均表明IIM相较IM有所优化,精度有所提升。
5 结论(1) 研究区灾害点布局分散,由因子探测结果可知,地形条件(植被覆盖度、地形起伏度)、人类工程活动(土地利用、距公路距离)所占权重较大,灾害多受其影响,且研究区灾害易发区不具有极端性,高易发区面积广泛。
(2) 耦合地理探测器确定指标因子权重,基于信息量法考虑非灾害点贡献信息量,构成加权模型。通过SCAI及ROC检验,对比IM,IIM,CF,IM-GD,CF-GD,IIM-GD模型在研究区划定的易发性分区结果较为精确,成功率为0.905,预测率为0.885,能够在该区域地质灾害危险性评价中起到较好的预测作用。
(3) 连续型因子不同的离散化方式、耦合模型类型等均可能对地理探测器结果产生影响,继而对加权后精度提升程度有所影响,未来研究可进一步探索使地理探测器结果产生差异的原因。并且,考虑非灾害点信息量在本研究区的易发性评价模型构建中成效显著,但是否具有普适性仍需进一步研究。
| [1] |
Liu Yu, Yuan Anying, Bai Zhigang, et al. GIS-based landslide susceptibility mapping using frequency ratio and index of entropy models for She County of Anhui Province, China[J]. Applied Rheology, 2022, 32(1): 22-33. DOI:10.1515/arh-2022-0122 |
| [2] |
Wu Bo, Zhao Fasuo, Wu Shaoyan, et al. A study of the relationship between fractal dimension of boundary trace and stability of the loess-bedrock landslide[J]. IOP Conference Series: Earth and Environmental Science, 2018, 186: 012044. |
| [3] |
罗路广, 裴向军, 崔圣华, 等. 九寨沟地震滑坡易发性评价因子组合选取研究[J]. 岩石力学与工程学报, 2021, 40(11): 2306-2319. Luo Luguang, Pei Xiangjun, Cui Shenghua, et al. Combined selection of susceptibility assessment factors for Jiuzhaigou earthquake-induced landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(11): 2306-2319. |
| [4] |
刘璐瑶, 高惠瑛, 李照. 基于CF与Logistic回归模型耦合的永嘉县滑坡易发性评价[J]. 中国海洋大学学报(自然科学版), 2021, 51(10): 121-129. Liu Luyao, Gao Huiying, Li Zhao. Landslide susceptibility assessment based on coupling of CF model and logistic regression model in Yongjia County[J]. Periodical of Ocean University of China, 2021, 51(10): 121-129. |
| [5] |
Asmare D. Application and validation of AHP and FR methods for landslide susceptibility mapping around choke mountain, Northwestern Ethiopia[J]. Scientific African, 2023, 19: e01470. DOI:10.1016/j.sciaf.2022.e01470 |
| [6] |
Abeysiriwardana H D, Gomes P I A. Integrating vegetation indices and geo-environmental factors in GIS-based landslide-susceptibility mapping: Using logistic regression[J]. Journal of Mountain Science, 2022, 19(2): 477-492. DOI:10.1007/s11629-021-6988-8 |
| [7] |
Gameiro S, Riffel E S, de Oliveira G G, et al. Artificial neural networks applied to landslide susceptibility: The effect of sampling areas on model capacity for generalization and extrapolation[J]. Applied Geography, 2021, 137: 102598. DOI:10.1016/j.apgeog.2021.102598 |
| [8] |
Hammad Khaliq A, Basharat M, Talha Riaz M, et al. Spatiotemporal landslide susceptibility mapping using machine learning models: A case study from district Hattian Bala, NW Himalaya, Pakistan[J]. Ain Shams Engineering Journal, 2023, 14(3): 101907. DOI:10.1016/j.asej.2022.101907 |
| [9] |
Chang Lili, Xing Gulian, Yin Hui, et al. Landslide susceptibility evaluation and interpretability analysis of typical loess areas based on deep learning[J]. Natural Hazards Research, 2023, 3(2): 155-169. DOI:10.1016/j.nhres.2023.02.005 |
| [10] |
常志璐, 黄发明, 蒋水华, 等. 基于多尺度分割方法的斜坡单元划分及滑坡易发性预测[J]. 工程科学与技术, 2023, 55(1): 184-195. Chang Zhilu, Huang Faming, Jiang Shuihua, et al. Slope unit extraction and landslide susceptibility prediction using multi-scale segmentation method[J]. Advanced Engineering Sciences, 2023, 55(1): 184-195. |
| [11] |
凌晓, 刘甲美, 王涛, 等. 基于致灾因子对称法分级的信息量模型在地震滑坡危险性评价中的应用[J]. 国土资源遥感, 2021, 33(2): 172-181. Ling Xiao, Liu Jiamei, Wang Tao, et al. Application of information value model based on symmetrical factors classification method in landslide hazard assessment[J]. Remote Sensing for Land & Resources, 2021, 33(2): 172-181. |
| [12] |
胡瑞林, 范林峰, 王珊珊, 等. 滑坡风险评价的理论与方法研究[J]. 工程地质学报, 2013, 21(1): 76-84. Hu Ruilin, Fan Linfeng, Wang Shanshan, et al. Theory and method for landslide risk assessment-current status and future development[J]. Journal of Engineering Geology, 2013, 21(1): 76-84. |
| [13] |
刘杰, 武震. 基于GIS的白龙江流域舟曲—武都段的滑坡危险性评价[J]. 地震工程学报, 2020, 42(6): 1723-1734. Liu Jie, Wu Zhen. Landslide risk assessment of the zhouqu-wudu section of bailong river basin based on geographic information system[J]. China Earthquake Engineering Journal, 2020, 42(6): 1723-1734. |
| [14] |
罗路广, 裴向军, 黄润秋, 等. GIS支持下CF与Logistic回归模型耦合的九寨沟景区滑坡易发性评价[J]. 工程地质学报, 2021, 29(2): 526-535. Luo Luguang, Pei Xiangjun, Huang Runqiu, et al. Landslide susceptibility assessment in Jiuzhaigou scenic area with GIS based on certainty factor and logistic regression model[J]. Journal of Engineering Geology, 2021, 29(2): 526-535. |
| [15] |
Dam N D, Amiri M, Al-Ansari N, et al. Evaluation of Shannon entropy and weights of evidence models in landslide susceptibility mapping for the pithoragarh district of uttarakhand state, India[J]. Advances in Civil Engineering, 2022, 2022: 1-16. |
| [16] |
梁丽萍, 刘延国, 唐自豪, 等. 基于加权信息量的地质灾害易发性评价: 以四川省泸定县为例[J]. 水土保持通报, 2019, 39(6): 176-182. Liang Liping, Liu Yanguo, Tang Zihao, et al. Geologic hazards susceptibility assessment based on weighted information value: A case study in Luding County, Sichuan Province[J]. Bulletin of Soil and Water Conservation, 2019, 39(6): 176-182. DOI:10.13961/j.cnki.stbctb.2019.06.026 |
| [17] |
陈飞, 蔡超, 李小双, 等. 基于信息量与神经网络模型的滑坡易发性评价[J]. 岩石力学与工程学报, 2020, 39(增刊1): 2859-2870. Chen Fei, Cai Chao, Li Xiaoshuang, et al. Evaluation of landslide susceptibility based on information volume and neural network model[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(Suppl.1): 2859-2870. |
| [18] |
Devkota K C, Regmi A D, Pourghasemi H R, et al. Landslide susceptibility mapping using certainty factor: Index of entropy and logistic regression models in GIS and their comparison at Mugling-Narayanghat Road section in Nepal Himalaya[J]. Natural Hazards, 2013, 65(1): 135-165. |
| [19] |
Shano L, Raghuvanshi T K, Meten M. Landslide susceptibility evaluation and hazard zonation techniques: A review[J]. Geoenvironmental Disasters, 2020, 7(1): 18. |
| [20] |
王昌明, 黄健, 李桥, 等. 基于信息量模型与Logistic回归模型耦合的山西吕梁市地质灾害易发性评价研究[J]. 水利水电技术, 2019, 50(3): 132-138. Wang Changming, Huang Jian, Li Qiao, et al. Evaluation of geological hazard vulnerability in Lyuliang City in Shanxi Province based on coupling of information content model and Logistic regression model[J]. Water Resources and Hydropower Engineering, 2019, 50(3): 132-138. |
| [21] |
黄强兵, 康孝森, 王启耀, 等. 山西吕梁黄土崩滑类型及发育规律[J]. 工程地质学报, 2016, 24(1): 64-72. Huang Qiangbing, Kang Xiaosen, Wang Qiyao, et al. Types and characteristics of loess landslides and collapses in l liang area of Shanxi Province[J]. Journal of Engineering Geology, 2016, 24(1): 64-72. |
| [22] |
周晓亭, 黄发明, 吴伟成, 等. 基于耦合信息量法选择负样本的区域滑坡易发性预测[J]. 工程科学与技术, 2022, 54(3): 25-35. Zhou Xiaoting, Huang Faming, Wu Weicheng, et al. Regional landslide susceptibility prediction based on negative sample selected by coupling information value method[J]. Advanced Engineering Sciences, 2022, 54(3): 25-35. |
| [23] |
魏江波, 赵洲. 基于加权确定性系数法的地质灾害易发性分析[J]. 煤田地质与勘探, 2018, 46(6): 108-114. Wei Jiangbo, Zhao Zhou. Analysis of geological hazard susceptibility based on the weighted certainty factor method[J]. Coal Geology & Exploration, 2018, 46(6): 108-114. |
| [24] |
杜宇琛, 葛永刚, 梁馨月, 等. 确定性系数与地理探测器模型耦合的泥石流易发性评估方法研究: 以安宁河流域为例[J]. 防灾减灾工程学报, 2022, 42(4): 664-673. Du Yuchen, Ge Yonggang, Liang Xinyue, et al. Research of debris flow susceptibility based on the coupling of certainty factor method and Geodetector model in Anning River basin[J]. Journal of Disaster Prevention and Mitigation Engineering, 2022, 42(4): 664-673. |
| [25] |
王劲峰, 徐成东. 地理探测器: 原理与展望[J]. 地理学报, 2017, 72(1): 116-134. Wang Jinfeng, Xu Chengdong. Geodetector: Principle and prospective[J]. Acta Geographica Sinica, 2017, 72(1): 116-134. |
| [26] |
Süzen M L, Doyuran V. A comparison of the GIS based landslide susceptibility assessment methods: Multivariate versus bivariate[J]. Environmental Geology, 2004, 45(5): 665-679. |
| [27] |
付树林, 梁丽萍, 刘延国. 基于CF-Logistic模型的雅砻江新龙段地质灾害易发性评价[J]. 水土保持研究, 2021, 28(4): 404-410. Fu Shulin, Liang Liping, Liu Yanguo. Assessment on geohazard susceptibility in Xinlong section of Yalong River based on CF-logistic model[J]. Research of Soil and Water Conservation, 2021, 28(4): 404-410. |
| [28] |
解明礼, 巨能攀, 赵建军, 等. 区域地质灾害易发性分级方法对比分析研究[J]. 武汉大学学报(信息科学版), 2021, 46(7): 1003-1014. Xie Mingli, Ju Nengpan, Zhao Jianjun, et al. Comparative analysis on classification methods of geological disaster susceptibility assessment[J]. Geomatics and Information Science of Wuhan University, 2021, 46(7): 1003-1014. |
| [29] |
罗路广, 裴向军, 黄润秋. 强震山区地震滑坡发生概率研究: 以九寨沟国家地质公园为例[J]. 岩石力学与工程学报, 2020, 39(10): 2079-2093. Luo Luguang, Pei Xiangjun, Huang Runqiu. Earthquake-triggered landslide occurrence probability in strong seismically mountainous areas: A case study of Jiuzhaigou National Geopark[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(10): 2079-2093. |
 2024, Vol. 44
2024, Vol. 44 

