水土流失是中国面临的主要环境问题之一[1]。据统计,2021年中国水土流失面积达到了2.67×106 km2[2]。研究表明,降雨是水土流失的主要动力[3]。一般来说,降雨强度和降雨量对水土流失的影响最大[3-4]。肖继兵等[5]研究发现I30与土壤侵蚀量之间存在显著的正相关关系。大量研究探索了不同降雨特征对土壤侵蚀量的影响。但定量描述降雨特征和土壤侵蚀量之间的关系对合理确定水保措施,降低水土流失具有更重要的现实意义。
目前,对不同降雨特征下土壤侵蚀量确定,主要采用传统的实地监测方法[3],但该方法成本较大。为此,一些学者使用模型对不同降雨特征下土壤水土流失量进行了预测模拟,其中最著名的5个传统物理和经验模型是修正的土壤流失方程(RUSLE)、通用土壤流失方程(USLE)、水土预测模型(WEPP),水土评估模型(SWAT)和水土侵蚀模型(WATEM)等[6]。Zhang Hua等[7]使用RUSLE模型基于降雨、土壤、植被覆盖、坡度和水土保持能力等5个参数,对兰州市水土流失量进行了模拟,并取得了良好的模拟效果。但该模型计算过程复杂,需要参数较多。综上所述,使用传统的监测和模型方法确定土壤侵蚀量具有成本高和过程复杂等缺点。近些年,随着机器学习算法的发展,并且机器学习模型能够有效拟合特征和目标变量之间的线性和非线性关系[8]。因而,一些学者开始使用机器学习模型对土壤侵蚀量进行预测。关于利用机器学习模型对土壤侵蚀量的研究也大致经历了3个阶段。第一阶段,众多学者开始关注单一机器学习模型对土壤侵量的预测。Rahmati等[9]比较了7个经典机器学习模型对土壤侵蚀量预测的精度,最终发现SVM模型对土壤侵蚀量预测精度最高。在这个阶段SVM模型在众多的研究中均取得了较高的精度[9]。第二阶段,考虑到单一机器学习模型虽然可以在预测土壤侵蚀量的任务中取得一定的精度,但不同的机器学习模型具有不同的特点。因此,大量研究开始关注集成学习模型对土壤侵蚀量的预测。通过不同的算法,将不同的机器学习模型进行集合。在此阶段使用较多方法是基于stacking,boosting和bagging算法对相同和不同机器学习模型进行集合[6]。Zhang Yonghong等[10]比较了XGBoost和单一经典模型对土壤侵蚀量的预测精度,发现XGBoost模型对土壤侵蚀量的预测精度最高。Nguyen等[6]将基于bagging算法的随机森林模型和基于boosting算法的GBM模型与传统的机器学习模型(线性回归、BP神经网络、SVM模型等)进行了比较,结果发现GBM模型对土壤侵蚀量的预测精度最高。在该阶段RF模型和基于boosting算法的集成学习模型取得了较高的预测精度。第三阶段,随着近些年深度学习模型的发展,如卷积神经网络、残差神经网络、循环神经网络等,一些学者开始探索深度学习模型对土壤侵蚀量的预测。但研究表明并非所有深度学习模型对土壤侵蚀量的预测结果均高于集成学习算法。如,Sahour等[8]使用多元线性回归模型、基于boosting的集成学习模型和深度学习模型对土壤侵蚀量进行了预测,结果发现基于boosting的集成学习模型预测土壤侵蚀量的精度最高。虽然使用机器学习模型对土壤侵蚀量的预测取得了一定的成果,但这些模型在预测土壤侵蚀量时,仅仅只考虑了当前的特征。实际上,降雨特征对土壤侵蚀量的影响具有累积效应,即土壤侵蚀量会受到历史降雨等特征的影响。为增加模型的预测精度,一些学者将前期的降雨或土壤特征作物特征输入预测当前的土壤侵蚀量,并且提高了模型的预测精度。但该方法增加了特征的选择难度,而且具有一定的经验性。实际上,土壤侵蚀量的预测是一个时间序列问题,因而使用擅长处理时间序列的机器学习模型,如循环神经网络(RNN)、长短期记忆神经网络(LSTM)等会提升模型对土壤侵蚀量的预测精度[11]。研究表明长短期记忆神经网络模型(LSTM)可以“记住”历史特征,因而在大量研究中取得了较高的精度,被认为是处理时序变量回归任务时的首选模型[12]。目前,LSTM模型在预测土壤侵蚀量的研究中仍不多见。另外,监测土壤侵蚀量的影响特征,如降雨量、降雨历时,最大30 min和60 min降雨强度也会增加工作量。因而探索基于少量重要特征对土壤侵蚀量进行精准预测,对降低成本和提高预测土壤侵蚀量效率具有重要意义。为探究LSTM模型利用重要降雨特征对土壤侵蚀量预测的可行性,本文以2011—2021年水土流失动态监测站数据为基础,首先综合评价了4个降雨特征(I30,I60,T和P)对于预测土壤侵蚀量的重要性。然后使用LSTM模型分别利用2个最重要的特征和全部4个特征对3种水保工程措施条件下土壤侵蚀量进行预测,并将预测结果与传统机器学习模型(BP,RF和SVM)预测的结果进行对比。以期为辽西北地区土壤侵蚀量的精准预测和合理制定水土保持措施提供理论和技术依据。
1 材料与方法 1.1 研究区概况与数据收集本研究基础数据(2011—2021年)来源于辽宁省朝阳市朝阳县东大道小流域全国水土流失动态监测站(120°01′00″E,41°26′00″N)。监测站平均降雨量、风速、气温分别为450 mm,2.9 m/s和8.2 ℃。监测站中有3个典型水保工程措施(监测小区),分别为水平槽、果树台田和梯田。径流小区内土壤为褐土,土壤容重为1.13 g/cm3。监测小区投影长度、宽度和坡度分别为20 m,5 m和12°。小区末端设有长度为5 m,宽度为0.6 m的集流槽,且流槽上缘与地面同高,确保小区地表径流汇入槽内。槽壁采用水泥抹面,确保水流面光滑;底部向下及向中间倾斜,保证水流顺利汇入分流桶。小区径流经集流槽流入分流桶,分流桶为砖混结构,根据当地降雨及产流情况,确定分流桶长宽高均为1 m,设1个分流孔。分流孔距分流桶底面60 cm。分流桶下方设置集流桶,规格为1 m×1 m×1 m,收集径流量较大时由分流桶流入的清水,下部设放水孔1处。每次降雨之后,测定分流桶深度,计算总的径流量。随后通过混匀样本,采用烘干法测定泥沙浓度,计算土壤流失量。气象数据由监测站附近的人工气象观测站及TRM-ZS2型自动气象站观测[13]。本研究中将间隔时间超过6 h的两次降雨,定义为两次降雨事件。通过对2011—2021年监测数据和侵蚀数据的整理,本文共计得到177条数据每条数据记录包含4个降雨特征(I30,I60,T和P)和土壤侵蚀量。本文中水平槽中土壤侵蚀量的最小值、最大值和标准差分别为0.34,17.15和5.89 kg;果树台田中为0.06,13.38,4.0 kg;梯田中为0.14,40.38,9.9 kg。该结果表明本研究土壤侵蚀量波动较大。
1.2 模型介绍随机森林模型(RF):随机森林是基于bagging集成算法的一种拓展[14]。它是在以决策树为基本学习器,使用bagging集成学习算法的基础上,进一步采用自助采样法对特征进行随机选择,使得由决策树构成的“森林”中每一棵“树”均不一样[15]。建立随机森林模型主要是对于决策树数量的选择及每一个决策树的内部结点数和叶结点数量的确定。因此本文在建模过程中主要是对这3个参数进行率定。支持向量机模型(SVM):支持向量机基本思路是将给定的数据集正确分开,同时使得不同类别之间的间隔最大化[16]。建立支持向量机模型时需要选择核函数gamma和损失参数C,因此本文对参数gamma和C进行率定。本文采用的BP神经网络是指含有2个隐含层的BP神经网络模型。前一层和后一层之间通过全连接方式连接。根据BP神经网络的原理,本文在建立BP神经网络模型时,选择Relu函数为激活函数[17]。这是因为Relu激活函数相比于传统的sigmoid函数,有效解决了梯度消失问题,同时还能使模型的收敛速度维持在一个稳定的范围之内[18-19]。
长短期记忆神经网络(LSTM):LSTM模型是经典的循环神经网络,且LSTM中的记忆单元能够“记住”历史信息,从而提高当前的预测精度。本文使用的长短期记忆神经网络结构图如图 1所示[20]。LSTM具体计算过程如公式(1)—(6)[11]:
| $f_t=\operatorname{sigmoid}\left(W_f h_{i-1}+U_f X_t+b_f\right) $ | (1) |
| $ i_t=\operatorname{sigmoid}\left(W_i h_{i-1}+U_i X_t+b_f\right) $ | (2) |
| $C_t^{\prime}=\tanh \left(W_c h_{i-1}+U_c X_t+b_c\right) $ | (3) |
| $C_t=f_t C_{t-1}+i_t C_t^{\prime}$ | (4) |
| $O_t=\operatorname{sigmoid}\left(W_0 h_{t-1}+U_0 X_t+b_0\right) $ | (5) |
| $ h_t=O_t \tanh \left(C_t\right)$ | (6) |
式中:sigmoid,tanh为激活函数;ft,it分别为考虑了t时间点的输入Xt和t-1时间点输出ht-1的结果; Ct′,Ct-1分别为忘记矩阵和记忆矩阵; Ct为新的记忆矩阵; Ot为没有进行选择的输出;ht为经过选择的最终输出。从公式(4)—(5)中可以看出, 最终的预测输出由Ot和Ct计算得到, 而Ot和Ct不仅与当前输入Xt有关, 也和上一个输出ht-1有关。因而, LSTM可以“历史”信息对当前的影响。另外, 由公式(4)和图 1中可以发现, 记忆矩阵Ct也在进行更新, 因而LSTM模型在不断训练会加强对重要信息的记忆。
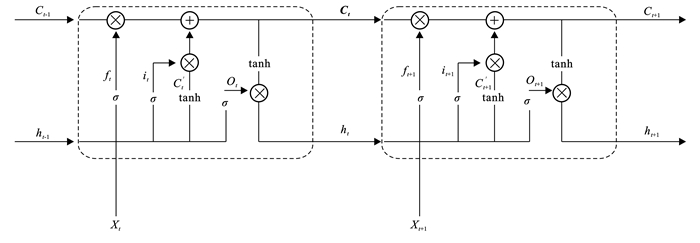
|
注:sigmoid,tanh为激活函数,ft,it分别为t时间点的输入Xt和t-1时间点输出ht-1的结果;Ct ′,Ct-1分别为忘记矩阵和记忆矩阵;Ct为新的控制矩阵;Ot为没有进行选择的初步输出;ht为进行选择后的最终输出。 图 1 LSTM模型基本结构 Figure 1 Structure of LSTM model |
本研究采用Python 3.0中Scikit-learn库对BP,RF和SVM模型进行建立和训练。本研究中,使用Python 3.0中TensorFlow 2库对LSTM模型进行建立和训练。本文中将收集到的177条记录分成训练集和测试集两个部分。首先根据80%训练集和20%训练集对总样本进行分割,同时考虑到本研究中样本数量较少,增加了测试样本量。最终确定训练集152条和测试集25条。另外,数据按时间序列排序分割。其中模型参数的选择使用3-折交叉验证的方法,即将训练集样本随机分成3份,依次取其中2份样本训练模型,剩下1份样本验证模型,最终选出合适的参数。采用相关系数(R2)和相对均方根误差(NRMSE)两个判断指标作为模型预测精度好坏的评价指标[12]。
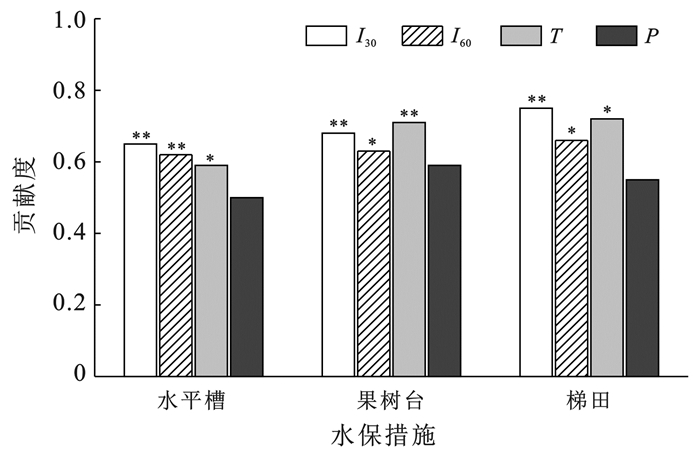
2 结果与讨论 2.1 基于随机森林的特征选择从图 2可知,研究区不同的水保措施下,I30,I60,T和P对土壤侵蚀量的影响程度不同。在水平槽中降雨因素对土壤侵蚀量的影响程度为:I30>I60>T>P;在果树台中降雨因素对土壤侵蚀量的影响程度为:T>I30>I60>P;在梯田中降雨因素对土壤侵蚀量的影响程度为:I30>T>I60>P。该结果与之前使用模糊贴近度法的计算结果类似[21]。
|
注:I30,I60,T和P分别为最大30 min和60 min降雨强度、降雨历时和降雨量。 图 2 研究区各特征因子对土壤侵蚀量的重要性程度 Figure 2 Importance of characteristic factors to soil erosion in study area |
由图 2还可以看出,I30,I60和T在3种水保措施中对土壤侵蚀量的影响均达到了显著水平。该结果与林锦阔等[4]研究结果类似,认为I30和降雨历时是影响土壤侵蚀量的主要原因。然而,陈钊柱等[3]研究发现降雨量与土壤侵蚀量之间存在显著的正相关关系。这种不一致的结果可能是由于降雨特征所在地区不同和土壤理化性质不同造成的[22]。综上所述,基于随机森林模型,I30,I60和T是该地区影响土壤侵蚀量的主要降雨特征。为了提高模型的预测精度,同时也为了降低监测降雨特征的工作量,本研究选择I30和T作为输入特征对土壤侵蚀量进行预测,并将该结果与使用全部4个降雨特征作为输入特征预测的土壤侵蚀量进行对比。
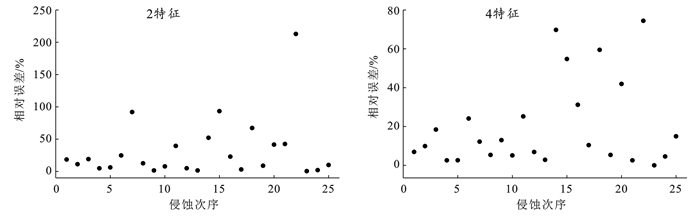
2.2 水平槽中土壤侵蚀量预测表 1列出了分别使用2个特征(I30和T)和4个特征(I30,I60,T和P)对研究区水平槽中土壤侵蚀量的预测精度。从表 1可以看出,BP模型在训练集和验证集上的NRMSE均大于0.2,表明BP模型对水平槽中土壤侵蚀量预测精度较低。RF和SVM模型在训练集和验证集上的NRMSE虽然小于0.2,但均大于0.15,表明RF和SVM模型在预测水平槽工程中土壤侵蚀量时精度一般。与RF和SVM模型相比,LSTM模型提高了R2约0.03~0.08,同时降低了NRMSE约0.04~0.08(表 1)。该结果说明,对于水平槽工程中土壤侵蚀量的预测,LSTM模型的精度最高。另外,LSTM模型在训练集和验证集上的NRMSE最大为0.12,最小为0.06,表明LSTM模型预测水平槽工程中土壤侵蚀量达到了较高的精度。在4个模型中,LSTM模型的精度最高,SVM和RF次之,BP模型最低。这是因为LSTM模型考虑了时间序列对水平槽工程中土壤侵蚀量的影响。在本研究中,LSTM模型考虑了前两次降雨对当前土壤侵蚀量的影响。该结果与Chen Zhijun等[12]研究结果类似,认为与传统机器学习模型(BP,RF,SVM和线性回归模型等)相比,深度学习模型(尤其是考虑时间变化的LSTM模型)对目标变量的预测精度更高。从表 1还可以看出,在仅使用I30和T两个特征时,在验证集上,LSTM模型对水平槽中预测土壤侵蚀量的NRMSE为0.11。在使用全部4个特征(I30,I60,T和P)时,LSTM模型水平槽工程中预测土壤侵蚀量的NRMSE为0.09。该结果表明,在增加两个特征后,LSTM模型的精度并未得到显著提高。从图 3中可以看出,在2特征和4特征情景中,虽然在一些观测点上LSTM预测的土壤侵蚀量与实测土壤侵蚀量之间的相对误差较大,但多数观测点上LSTM模型的预测值与实测值之间误差较低,且总体上误差也在可接受范围内(表 1)。LSTM模型在一些观测点上产生较大的相对误差,这可能是因为样本数据中土壤侵蚀量波动较大。从图 3还可以看出,虽然基于4特征的LSTM模型的相对误差较小,但基于2特征的LSTM模型总体误差也较低(表 1)。因此,在水平槽工程中LSTM模型使用I30和T这2个特征可以较准确预测土壤侵蚀量。这是因为在水平槽工程中,I30和T对土壤侵蚀量具有显著影响。综上所述,在水工槽中,相比于BP,RF和SVM模型,LSTM模型对土壤侵蚀量的预测精度最高。同时,LSTM使用I30和T作为特征和使用全部4个特征(I30,I60,T和P)对土壤侵蚀量的预测精度没有显著差异。
|
|
表 1 各模型在研究区水平槽中预测土壤侵蚀量的精度 Table 1 Precision of models in predicting soil erosion of horizontal channel in study area |
|
图 3 研究区水平槽中LSTM模型预测值与实测值对比 Figure 3 Comparison between LSTM-predicted value and measured value of horizontal channel in study area |
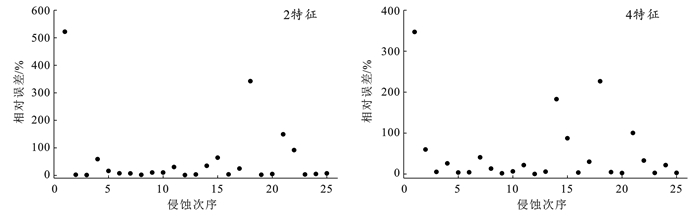
表 2列出了在果树台田措施中,各模型预测土壤侵蚀量的R2和NRMSE。从表 2可以看出,在果树台田措施中,BP模型在训练集和验证集上的R2为0.83~0.84,处于较高水平,表明BP模型预测的土壤侵蚀量的趋势与实测土壤侵蚀量的趋势较为一致。但BP模型在训练集和验证集上的NRMSE较大,均大于0.2。该结果说明使用BP模型预测果树台田措施中土壤侵蚀量的误差较大。RF和SVM模型的预测精度相近,在预测果树台田措施中土壤侵蚀量的R2和NRMSE分别为0.87~0.91,0.12~0.19。该结果表明RF和SVM模型的预测精度较好。与RF和SVM模型相比,LSTM模型提高了R2约0.08~0.11和降低了NRMSE约0.02~0.08。该结果说明LSTM模型对果树台田措施中土壤侵蚀量的预测精度最高。传统的机器学习模型,如BP,RF和SVM,在预测土壤侵蚀量时仅考虑了本次降雨特征对土壤侵蚀量影响。而LSTM模型通过内部的记忆单元可以记住之前降雨特征对土壤侵蚀量的影响。在实际中,前一次降雨对土壤的侵蚀会影响下一场降雨对土壤侵蚀量的影响,尤其是两次降雨事件接近时。因此,LSTM在众多时序数据的预测研究中取得了较高的精度[22]。在使用2特征和4特征情景中,LSTM模型在验证集上的R2均为0.99,说明LSTM模型能够很好地预测土壤侵蚀量的变化趋势。这是因为在实际中,降雨特征与土壤侵蚀侵蚀量之间的线性关系较强,而LSTM模型能够通过时间序列的记忆,很好地处理线性和非线性关系[23]。但LSTM在2特征和4特征情景中预测果树台中土壤侵蚀量的NRMSE均大于0.1。该结果说明,LSTM在预测精度方面不如预测趋势精确。但是,LSTM在2特征和4特征情景中预测果树台中土壤侵蚀量的NRMSE分别为0.13,0.11,说明LSTM对果树台中土壤侵蚀量的预测精度较高。同时,使用2特征和4特征对土壤侵蚀量预测的精度类似。从图 4也可以看出,LSTM模型在2特征和4特征情景中对土壤侵蚀量预测的相对误差相近。虽然在有些观测点上相对误差较大,但多数点的相对误差较低。该结果说明,LSTM模型使用2个特征预测土壤侵蚀量时精度较好。LSTM模型使用4个特征预测土壤侵蚀量的精度并没有显著优于使用2个特征预测土壤侵蚀量的精度。这可能是因为:①本研究中使用的两个特征(I30和T)是影响果树台田措施中土壤侵蚀量的主要降雨特征(图 2);②4个降雨特征I30,I60,T和P之间存在相关性,因此有些特征对于预测土壤侵蚀量来说是冗余信息[24]。综上所述,在果树台田措施中,LSTM模型的预测精度最高。同时,LSTM仅使用最重要的两个降雨特征(I30和T)即可较准确地预测土壤侵蚀量。
|
|
表 2 各模型在果树台田中预测土壤侵蚀量的精度 Table 2 Precision of models in predicting soil erosion of fruiter terrace lands |
|
图 4 果树台田中LSTM模型预测值与实测值对比 Figure 4 Comparison between LSTM-predicted value and measured value of fruiter terrace lands |
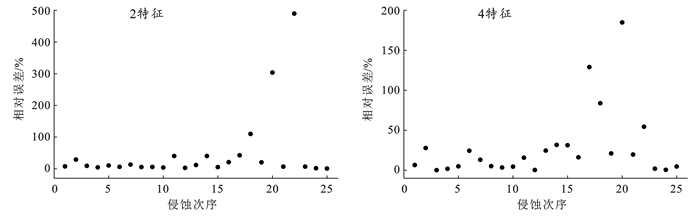
表 3列出了BP,RF,SVM和LSTM模型对梯田中土壤侵蚀量的预测精度。从表 3可以看出,4个模型预测梯田中土壤侵蚀量的R2均大于0.79。该结果说明,4个模型均能很好预测梯田中土壤侵蚀量的变化趋势。但BP模型在训练集和验证集上预测梯田中土壤侵蚀量的NRMSE均大于0.2,说明BP模型对梯田中土壤侵蚀量的预测精度较低。与在水平槽和果树台田措施中类似,在梯田中RF和SVM模型的预测精度相近。从表 3可以看出,RF和SVM模型预测梯田中土壤侵蚀量的NRMSE均相差0.01~0.03。与大多数结果一致,在传统机器学习模型中,RF和SVM模型在回归和分类任务中均取得了较高的精度[25]。但与深度学习模型相比,RF和SVM模型的精度较低。相比于RF和SVM模型,LSTM模型降低了NRMSE约0.05~0.08(表 3)。主要原因与在水平槽和果树台中类似:LSTM模型通过长短期记忆单元,在预测土壤侵蚀量的同时不仅考虑了本次降雨特征的影响,还考虑了之前降雨特征的影响[25]。此外,在2特征和4特征情景中,LSTM模型预测梯田中土壤侵蚀量的NRMSE分别为0.12,0.09。该结果表明,相比于2特征情景,在4特征情景中LSTM模型预测梯田中的土壤侵蚀量提高了0.03。从图 5也可以看出,LSTM模型使用2特征和4特征预测的梯田土壤侵蚀量与实测值之间差异分别为0.65%~489.7%和0.18%~184.8%。LSTM模型在一些观测点上产生较大的相对误差,这可能是因为样本数据中土壤侵蚀量波动较大。但总体上LSTM使用2个重要降雨特征(I30和T)预测梯田中土壤侵蚀量时,仍然取得了较高的精度(表 3)。一方面,I30和T是影响梯田中土壤侵蚀量最重要的两个特征。另一方面,降雨特征之间存在线性相关。例如,I30和I60之间通常存在显著的正相关关系[5]。综上所述,在梯田中,相比于传统的机器学习模型,LSTM模型预测土壤侵蚀量的精度最高。同时,基于LSTM模型,使用I30和T可以较为准确地预测土壤侵蚀量。
|
|
表 3 各模型在梯田中预测土壤侵蚀量的精度 Table 3 Precision of models in predicting soil erosion of terrace |
|
图 5 梯田中LSTM模型预测值与实测值对比 Figure 5 Comparison between LSTM-predicted value and measured value of terrace |
以2011—2021年水土流失动态监测站数据为基础,首先综合评价了4个降雨特征(I30,I60,T和P)对于预测土壤侵蚀量的重要性。然后使用LSTM模型分别利用2个最重要的特征(I30和T)和全部4个特征分别对3种水保工程措施条件下土壤侵蚀量进行预测。主要结论为:
(1) 在水平槽、果树台田和梯田3种水保工程措施中,I30,I60和T对土壤侵蚀量有显著影响;
(2) 在水平槽、果树台田和梯田3种水保工程措施中,使用I30,I60,T和P变量时,LSTM模型对土壤侵蚀量的预测精度最高,RF和SVM次之,BP模型最低;
(3) 在水平槽、果树台田和梯田3种水保工程措施中,仅使用I30和T两个变量,LSTM模型对土壤侵蚀量的预测取得了较高的精度。综上所述,LSTM模型在辽西北地区水平槽、果树台和梯田3种水保工程措施中,对土壤侵蚀量的预测精度高于传统的神经网络、支持向量机和随机森林模型,为辽西北地区合理制定水土保持措施提供理论和技术依据。
| [1] |
Zhao Jianlin, Wang Zhengang, Dong Yifan, et al. How soil erosion and runoff are related to land use, topography and annual precipitation: insights from a meta-analysis of erosion plots in China[J]. Science of the Total Environment, 2022, 802: 149665. DOI:10.1016/j.scitotenv.2021.149665 |
| [2] |
于珊. 我国水土流失面积和强度继续保持"双降"[OL]. 北京: 新华社, 2022-06-28. http://www.gov.cn/xinwen/2022-06/28/content_5698072.htm.
|
| [3] |
陈钊柱, 蔡卓杰, 谢福倩, 等. 自然降雨对广西赤红壤坡地土壤侵蚀特征的影响[J]. 水土保持通报, 2022, 42(3): 36-42. |
| [4] |
林锦阔, 李子君, 许海超, 等. 降雨因子对沂蒙山区不同土地利用方式径流小区产流产沙的影响[J]. 水土保持通报, 2016, 36(5): 7-12. |
| [5] |
肖继兵, 孙占祥, 蒋春光, 等. 辽西地区农耕坡地土壤侵蚀影响因素及相关关系[J]. 水土保持学报, 2015, 29(5): 13-19. |
| [6] |
Nguyen K A, Chen W, Lin B S, et al. Comparison of ensemble machine learning methods for soil erosion pin measurements[J]. Isprs International Journal of Geo-Information, 2021, 10(1): 42. DOI:10.3390/ijgi10010042 |
| [7] |
Zhang Hua, Lei Jinping, Wang Hao, et al. Study on dynamic changes of soil erosion in the North and South Mountains of Lanzhou[J]. Water, 2022, 14(15): 2388. DOI:10.3390/w14152388 |
| [8] |
Sahour H, Gholami V, Vazifedan M, et al. Machine learning applications for water-induced soil erosion modeling and mapping[J]. Soil and Tillage Research, 2021, 211: 105032. DOI:10.1016/j.still.2021.105032 |
| [9] |
Rahmati O, Tahmasebipour N, Haghizadeh A, et al. Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion[J]. Geomorphology, 2021, 298: 118-137. |
| [10] |
Zhang Yonghong, Ge Taotao, Tian Wei, et al. Debris flow susceptibility mapping using machine-learning techniques in Shigatse area, China[J]. Remote Sensing, 2019, 11(23): 2801. DOI:10.3390/rs11232801 |
| [11] |
Senanayake S, Pradhan B, Alamri A, et al. A new application of deep neural network(LSTM) and RUSLE models in soil erosion prediction[J]. Science of The Total Environment, 2022, 845: 157220. |
| [12] |
Chen Zhijun, Zhu Zhenchuang, Jiang Hao, et al. Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods[J]. Journal of Hydrology, 2020, 591: 125286. |
| [13] |
李明伟. 辽西地区不同水土保持措施条件下土壤侵蚀量与降雨因子关系研究[J]. 中国水土保持, 2018(8): 29-33. |
| [14] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
|
| [15] |
王升, 付智勇, 陈洪松, 等. 基于随机森林算法的参考作物蒸发蒸腾量模拟计算[J]. 农业机械学报, 2017, 48(3): 302-309. |
| [16] |
Dinh T V, Nguyen H, Tran X L, et al. Predicting rainfall-induced soil erosion based on a hybridization of adaptive differential evolution and support vector machine classification[J]. Mathematical Problems in Engineering, 2021, 2021: 1-20. |
| [17] |
冯禹, 崔宁博, 龚道枝, 等. 利用温度资料和广义回归神经网络模拟参考作物蒸散量[J]. 农业工程学报, 2016, 32(10): 81-89. |
| [18] |
Alhassan A M, Zainon W M N W. Brain tumor classification in magnetic resonance image using Hardswish-based RELU activation function-convolutional neural network[J]. Neural Computing and Applications, 2021, 33(15): 9075-9087. |
| [19] |
张焕, 张庆, 于纪言. 激活函数的发展综述及其性质分析[J]. 西华大学学报(自然科学版), 2021, 40(4): 1-10. |
| [20] |
刘定一, 沈阳阳, 詹天明, 等. 融合微博热点分析和LSTM模型的网络舆情预测方法[J]. 江苏大学学报(自然科学版), 2021, 42(5): 546-553. |
| [21] |
刘洁, 陈晓宏, 许振成, 等. 降雨变化对东江流域径流的影响模拟分析[J]. 地理科学, 2015, 35(4): 483-490. |
| [22] |
Zha Wenshu, Liu Yuping, Wan Yujin, et al. Forecasting monthly gas field production based on the CNN-LSTM model[J]. Energy, 2022, 260: 124889. |
| [23] |
任雨之, 郑江坤, 付滟, 等. 不同耕种模式下降雨等级对紫色土坡耕地产流产沙的影响[J]. 中国水土保持科学, 2020, 18(3): 90-98. |
| [24] |
Feng Ziyi, Huang Guanhua, Chi Daocai. Classification of the complex agricultural planting structure with a semi-supervised extreme learning machine framework[J]. Remote Sensing, 2020, 12(22): 3708. |
| [25] |
陈英义, 程倩倩, 方晓敏, 等. 主成分分析和长短时记忆神经网络预测水产养殖水体溶解氧[J]. 农业工程学报, 2018, 34(17): 183-191. |
 2023, Vol. 43
2023, Vol. 43 
