2. 水利部 黄河下游河道与河口治理重点实验室, 河南 郑州 450003
2. Key Laboratory of Lower Yellow River Channel and Estuary Regulation, Ministry of Water Resources, Zhengzhou, Henan 450003, China
水资源是社会经济发展与生态环境维持的物质基础和重要保障。现阶段,随着水资源开发利用程度的提高,水资源短缺问题逐渐暴露并成为制约区域可持续发展的重要因素[1]。因此,专家学者们采用不同的研究方法对水资源生态压力和可持续利用状况开展了大量研究,包括生态足迹法[2]、集对分析法[3]、人工神经网络法[4]和模糊综合评价法等[5]。其中生态足迹法因综合性、普适性和客观性较强,且能够定量评估区域水资源消耗程度及可承载状态而被广泛应用[6]。
生态足迹模型由Rees等首次提出,并发展成为量度资源可持续性的有效核算工具[7-8],其后被引入国内并逐步应用于水资源的核算评价与战略研究中[9-10]。黄林楠等[11]确定了水资源生态足迹模型计算所需参数并根据用水特性对水资源账户进行了划分;杜轶等[12]分别基于国家公顷法和全球公顷法核算山西省水资源生态足迹,认为应根据不同的研究目的构建相应计算模型进行水资源生态足迹的分析;马剑锋等[13]运用该模型并结合对数均值迪式指数分解法(logarithmic mean Divisia index,LMDI)对中国西北干旱区水资源生态足迹的变化特征及影响机制进行分析;金昌盛等[14]基于该模型测算长江经济带各省(市)的水资源生态足迹并通过灰色预测模型GM(1, 1)对未来变化趋势进行预测。上述研究分别为相关地区的水资源可持续利用状况提供了参考,然而针对黄河下游地区的水资源生态足迹研究还较少。
黄河下游地区是黄河流域的经济发展高地,人口众多,产业密集,规模以上企业数量约占整个流域的66%[15],此外,黄河下游是我国重要的粮食产地,引黄灌区多,用水需求大,有中国最大连片自流灌区之称[16]。水资源匮乏导致的供需失衡已成为维系该区域可持续发展的主要瓶颈[17],在“黄河流域生态保护和高质量发展”已提升为重大国家战略的当下,亟待对占据着黄河流域极为重要位置的下游地区进行水资源可持续性研究[18]。因此,本文运用水资源生态足迹理论结合对数均值迪式指数分解法对2007—2020年黄河下游水资源生态足迹的时空分布特征及驱动机制进行核算分析,并通过灰色预测模型GM(1, 1)对未来10 a的水资源生态足迹变化趋势进行预测,以期为黄河下游水资源管理与规划提供理论依据。
1 研究区域与研究方法 1.1 研究区域与数据来源 1.1.1 研究区域黄河下游始自郑州桃花峪,终至东营黄河入海口,干流全长786 km,沿岸城市众多。本文以黄河下游沿岸郑州、焦作、开封、新乡、濮阳、菏泽、济宁、泰安、聊城、济南、德州、淄博、滨州、东营共14座城市作为研究区域(34°15′—38°10′N,112°33′—119°18′E)。该区域属于温带季风气候,多年(2007—2020年)平均降雨量619.7 mm,2020年总人口8.53×107人、GDP总量5.66×1012元。
1.1.2 数据来源本研究所需黄河下游14座地级市的人口、面积、GDP、水资源总量、用水量等数据来源于相关省市的水资源公报、统计年鉴等文献。
1.2 水资源生态足迹模型 1.2.1 水资源生态足迹水资源生态足迹是指将区域生产生活和生态系统健康维持所消耗的水资源量换算为生产相应账户水资源所需的用地面积[19]。本文结合水资源生态足迹的内涵和研究区域所在省市的水资源统计口径,将水资源生态足迹账户划分为农业用水、工业用水和城乡生活环境用水3类。计算公式为:
| $ {\rm{EF}} = \sum\limits_{i = 1}^3 {{\rm{E}}{{\rm{F}}_i}} = \sum\limits_{i = 1}^3 N \cdot {\rm{e}}{{\rm{f}}_i} = \sum\limits_{i = 1}^3 N \cdot \gamma \cdot \left( {{W_i}/P} \right) $ | (1) |
式中:EF为水资源总生态足迹(hm2); EFi为第i类水资源生态足迹(hm2); N为区域总人口(万人); efi为第i类人均水资源生态足迹(hm2/人); γ为水资源全球均衡因子, 取值5.19[11]; Wi为第i类水资源人均消耗量(m3); P为全球水资源平均生产能力, 取值3 140 m3/hm2[11]。
1.2.2 水资源生态承载力水资源生态承载力是指区域水资源供给量对社会经济和生态环境系统良性发展的支撑能力[20],计算公式为:
| $ {\rm{EC}} = N \cdot {\rm{ec}} = N \cdot (1 - \alpha ) \cdot \varphi \cdot \gamma (Q/P) $ | (2) |
式中:EC为水资源生态承载力(hm2); ec为人均水资源生态承载力(hm2/人); Q为人均区域水资源总量(m3); 区域水资源承载力的60%需用于生态环境的维持[21], 因此α取值0.6; φ为水资源产量因子, 取区域水资源平均生产能力与全球水资源平均生产能力的比值[11], 由2007—2020年水资源统计数据核算得到黄河下游城市郑州、焦作、开封、新乡、濮阳、菏泽、济宁、泰安、聊城、济南、德州、淄博、滨州、东营的水资源产量因子分别为0.38, 0.59, 0.51, 0.45, 0.38, 0.52, 0.56, 0.52, 0.45, 0.63, 0.58, 0.62, 0.39, 0.24, 下游整体水资源产量因子为0.49。
1.2.3 水资源生态盈余/赤字评价区域水资源可持续利用程度[22],计算公式为:
| $ {\rm{EB}} = {\rm{EC}} - {\rm{EF}} $ | (3) |
式中:EB为水资源生态盈亏指数(hm2); 其值为正, 表明区域生态盈余, 尚有水资源开发空间; 其值为0, 表明区域水资源生态平衡; 其值为负, 表明区域生态赤字, 水资源开发过量。
1.2.4 水资源生态足迹强度衡量区域水资源利用效率,其值越高(低)表明水资源利用效率越低(高)[23],计算公式为:
| $ {\rm{EG}} = {\rm{EF}}/y $ | (4) |
式中:EG为水资源生态足迹强度(hm2); y为区域生产总值GDP(万元)。
1.3 基于LMDI的水资源生态足迹分解模型对数均值迪式指数分解法(LMDI)是因素分解法的重要分支之一,因其克服了分解研究中的“0”值和“剩余”问题而得到广泛应用[24]。水资源生态足迹的LMDI分解模型为:
| $ {\rm{e}}{{\rm{f}}_t} = \sum\limits_{i = 1}^3 {{\rm{e}}{{\rm{f}}_{it}}} = \sum\limits_{i = 1}^3 {\frac{{{\rm{e}}{{\rm{f}}_{it}}}}{{{\rm{e}}{{\rm{f}}_t}}}} \frac{{{\rm{e}}{{\rm{f}}_t}}}{{{y_t}}}\frac{{{y_t}}}{{{N_t}}}{N_t} = \sum\limits_{i = 1}^3 {{s_{it}}} {i_t}{r_t}{N_t} $ | (5) |
| $ \begin{array}{l} \Delta {\rm{e}}{{\rm{f}}_t} = {\rm{e}}{{\rm{f}}_t} + {\rm{e}}{{\rm{f}}_0} = \sum\limits_{i = 1}^3 {{s_{it}}} {i_t}{r_t}{N_t} - \sum\limits_{i = 1}^3 {{s_{i0}}} {i_0}{r_0}{N_0}\\ \;\;\;\;\;\;\; = \Delta {\rm{e}}{{\rm{f}}_s} + \Delta {\rm{e}}{{\rm{f}}_i} + \Delta {\rm{e}}{{\rm{f}}_r} + \Delta {\rm{e}}{{\rm{f}}_N} \end{array} $ | (6) |
式中:eft为t年人均水资源生态足迹(hm2·人); efit为t年第i类人均水资源生态足迹(hm2/人); yt为t年区域生产总值GDP(亿元); Nt为t年区域人口数(万人); ef0为基准年(2007年)人均水资源生态足迹(hm2/人); Δefs,Δefi,Δefr,ΔefN分别表示结构因素、技术因素、经济因素和人口因素引起的人均水资源生态足迹的变化量(hm2/人)。
| $ \Delta {\rm{e}}{{\rm{f}}_s} = \sum\limits_{i = 1}^3 {\left( {\frac{{{\rm{e}}{{\rm{f}}_{it}} - {\rm{e}}{{\rm{f}}_{i0}}}}{{{\rm{lne}}{{\rm{f}}_{{\rm{it}}}} - \ln e{f_{i0}}}}\ln \frac{{{s_{it}}}}{{{s_{i0}}}}} \right)} $ | (7) |
| $ \Delta {\rm{e}}{{\rm{f}}_i} = \ln \frac{{{i_t}}}{{{i_0}}}\sum\limits_{i = 1}^3 {\frac{{{\rm{e}}{{\rm{f}}_{it}} - {\rm{e}}{{\rm{f}}_{i0}}}}{{{{{\mathop{\rm lnef}\nolimits} }_{it}} - {{{\mathop{\rm lnef}\nolimits} }_{i0}}}}} $ | (8) |
| $ \Delta {\rm{e}}{{\rm{f}}_r} = \ln \frac{{{r_t}}}{{{r_0}}}\sum\limits_{i = 1}^3 {\frac{{{\rm{e}}{{\rm{f}}_{it}} - {\rm{e}}{{\rm{f}}_{i0}}}}{{{{{\mathop{\rm lnef}\nolimits} }_{it}} - {{{\mathop{\rm lnef}\nolimits} }_{i0}}}}} $ | (9) |
| $ \Delta {\rm{e}}{{\rm{f}}_N} = \ln \frac{{{N_t}}}{{{N_0}}}\sum\limits_{i = 1}^3 {\frac{{{\rm{e}}{{\rm{f}}_{it}} - {\rm{e}}{{\rm{f}}_{i0}}}}{{{{{\mathop{\rm lnff}\nolimits} }_{it}} - {{{\mathop{\rm lnef}\nolimits} }_{i0}}}}} $ | (10) |
式中:Sit, it, rt分别对应
灰色预测模型GM(1, 1)通过对原始数据作累加生成处理得到具有近似指数规律的数列,再进行建模的方法进行数据预测,是线性时间序列预测的主要工具之一,其相比于传统预测方法有着样本量要求少、计算简便、相对误差小、预测精度高等优点,目前已得到广泛应用[25-27]。其基本形式为:
(1) 记需要预测的原始数列为X(0)=X(0)(1), X(0)(2)…X(0)(n),对X(0)做一次累加生成得X(1)=X(1)(1), X(1)(2)…X(1)(n),其中:
| $ \begin{array}{l} {X^{(1)}}(k) = \sum\limits_{i = 1}^k {{X^{(0)}}} (i)\\ \;\;\;\;\;\;\;\;\;\;\;\;(k = 1, 2 \cdots n;i = 1, 2 \cdots n) \end{array} $ | (11) |
(2) 对原始数列进行级比检验:
| $ {\rho _k} = \frac{{{X^{(0)}}(k - 1)}}{{{X^{(0)}}(k)}}\quad (k = 2 \cdots n) $ | (12) |
若ρk值均处于可容性覆盖区间(e-2/n+1, e2/n+1)内则符合预测条件;否则应选取适合的常数b对原始数据做平移转换处理〔公式(13)〕,使处理后的数列Y(0)=Y(0)(1), Y(0)(2)…Y(0)(n)的级比值处于可容性覆盖区间内。
| $ {Y^{(0)}}(k) = {X^{(0)}}(k) + b $ | (13) |
(3) 通过累加生成序列X(1)建立GM(1, 1)模型的一阶微分方程:
| $ \frac{{{\rm{d}}{X^{(1)}}}}{{{\rm{d}}t}} + \alpha {X^{(1)}} = \mu $ | (14) |
发展系数α和灰色作用量μ通过最小二乘法求解,设:
| $ a = {(\alpha , \mu )^T} = {\left( {{B^T}B} \right)^{ - 1}}{B^T}D $ | (15) |
其中
| $ B = \left[ {\begin{array}{*{20}{c}} { - 0.5\left[ {{X^{(1)}}(2) + {X^{(1)}}(1)} \right]}&1\\ \vdots & \vdots \\ { - 0.5\left[ {{X^{(1)}}(n) + {X^{(1)}}(n - 1)} \right]}&1 \end{array}} \right] $ | (16) |
| $ D = {\left[ {{X^{(0)}}(2) \cdots {X^{(0)}}(n)} \right]^T} $ | (17) |
对式(14)和式(15)求解得:
| $ {\hat X^{(1)}}(k + 1) = \left[ {{X^{(0)}}(1) - \frac{\mu }{\alpha }} \right]{{\rm{e}}^{ak}} + \frac{\mu }{\alpha } $ | (18) |
对累加值
| $ {\hat X^{(0)}}(k + 1) = {\hat X^{(1)}}(k + 1) - {\hat X^{(1)}}(k) $ | (19) |
(4) 后验差检验:
| $ C = {S_1}/{S_2} $ | (20) |
| $ P = \left\{ {\left| {{{\rm{\Delta }}^{(0)}}(k) - {{{\rm{\bar \Delta }}}^{(0)}}} \right|} \right\} < 0.6745{S_1} $ | (21) |
式中:C为方差比; P为小概率误差; S1为原始数据标准差; S2为残差标准差; Δ(0)(k)为原始数列残差; Δ(0)为残差平均值。C值及P值与预测模型精度关联情况见表 1。
|
|
表 1 后验差检验等级划分 Table 1 Classification of post acceptance test |
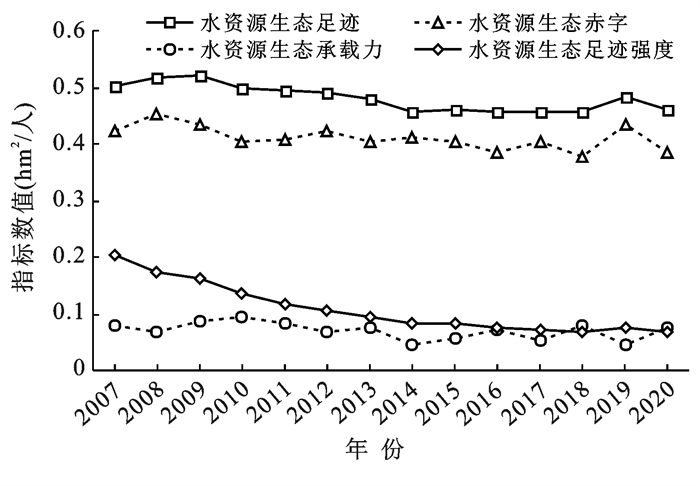
由公式(1)—(4)核算得到2007—2020年黄河下游人均水资源生态足迹和生态承载力,并在此基础上得出区域人均水资源生态盈亏和生态足迹强度(图 1)。黄河下游人均水资源生态足迹保持在0.455~0.521 hm2/人之间,历年均值为0.480 hm2/人,最低和最高值分别出现在2009,2014年;时间动态上来看,2007—2020年呈波动下降趋势,降幅达8.73%。受限于黄河下游区域低水资源总量和低产量因子,人均水资源生态承载力相对较低,历年均值仅为0.070 hm2/人,各年间在0.045~0.093 hm2/人之间波动变化,最低和最高值分别出现在2014年、2010年。区域人均水资源生态足迹远高于生态承载力,水资源的超载使用导致出现水资源生态赤字现象,人均水资源生态赤字范围在0.376~0.451 hm2/人之间,历年均值0.410 hm2/人,最低和最高值分别出现在2008,2018年;年际间变化趋势与水资源生态足迹的变化趋势较为相似,2020年的人均生态赤字值相较于2007年下降了8.73%,表明区域水资源可承载状态及可持续利用状况相对好转。人均水资源生态足迹强度近年来显著下降,历年均值为0.095 hm2/人,2007年最高达0.203 hm2/人,至2020年降为0.069 hm2/人,年均降幅5.08%,这表明在区域生产力快速发展与经济结构优化调整等的影响下,用水效率逐渐提高。
|
图 1 2007—2020年黄河下游人均水资源状况变化趋势 Figure 1 Change trend of per capita water resources in the lower reaches of the Yellow River basin from 2007 to 2020 |
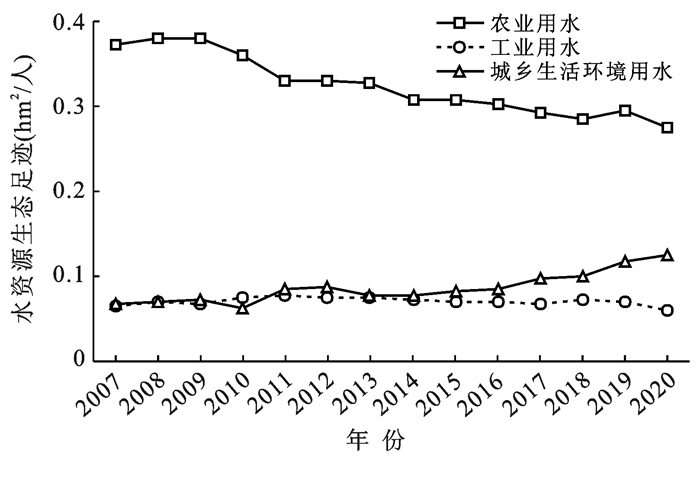
黄河下游水资源生态足迹构成如图 2所示。黄河下游灌区是中国重要的产粮基地之一[28],农业生产用水是黄河下游最主要的用水方式,2007—2020年人均农业用水足迹均值为0.323 hm2/人,占总水资源足迹的67.29%;时间线上来看,人均农业用水足迹显著下降,2007—2020年间共下降0.103 hm2/人,降幅达27.39%。在黄河下游城市农业种植面积相对稳定的发展背景下[29],区域水资源刚性约束下的农业集约化用水和节水灌溉技术的发展是农业用水足迹下降和用水效率提高的主要原因。2007—2020年人均工业用水足迹均值为0.070 hm2/人,在总用水足迹中占比最低(仅为14.58%),最低值为2020年的0.060 hm2/人,最高值为2011年的0.078 hm2/人;年际间呈现先升高后降低的变化规律,表明近年来工业结构升级和绿色低耗转型已见成效[18]。2007—2020年人均城乡生活环境用水足迹均值为0.087 hm2/人,占总用水足迹的18.13%;与农业和工业用水足迹近年来呈下降趋势相反,城乡生活环境用水呈波动上升趋势,2020年达到0.124 hm2/人,较2007年增加了85.33%,区域用水结构显著优化。
|
图 2 2007—2020年黄河下游人均水资源生态足迹构成 Figure 2 Composition of the per capita ecological footprint of water resources in the lower reaches of the Yellow River basin from 2007 to 2020 |
众多学者基于该模型对中国其他地区水资源生态足迹状况也做了大量研究。与黄河下游地区相似,黄河沿线九省区历年间(2006—2018年)人均水资源生态足迹也呈现整体下降趋势,此外,除四川省和青海省外的其他沿黄七省区亦均处于水资源生态赤字状态,可持续发展压力较大[22]。而长江经济带各省市(2004—2015年)人均水资源生态足迹则呈现先上升后趋于平稳的整体变化趋势,造成上述差异的原因在于黄河沿岸省市人均工农业等生产用水量逐渐降低,而长江经济带生产用水量逐渐增加,但由于长江经济带更高的水资源禀赋条件,该地区依然处于水资源生态盈余状况,可持续发展潜力较大[14]。
2.2 黄河下游水资源生态足迹与生态承载力空间分布特征为直观反映黄河下游水资源状况的空间分布特征,分别以2007—2009年作为基准年、2018—2020年作为现状年进行各城市的指标核算,各城市人均水资源生态足迹和生态盈亏的时空分布格局有着显著差异(图 3a与图 3b)。现状年间,东营人均水资源生态足迹和生态赤字最高(分别为1.033 hm2/人和0.954 hm2/人),滨州人均水资源生态足迹和生态赤字次之(分别为0.757 hm2/人和0.675 hm2/人),这表明黄河三角洲是黄河下游水资源超负载最严重区域,区域经济社会发展的客水依赖程度最高,可持续发展状况最差,亟待优化产业布局,推进节水建设,加强水资源管理与利用。人均水资源生态足迹最低的城市依次为郑州、泰安、济南和淄博,分别为0.282,0.341,0.356,0.358 hm2/人。人均水资源生态赤字最低的城市分别为淄博、泰安、济南和郑州,分别为0.228,0.238,0.259,0.267 hm2/人。区域人均水资源生态足迹和生态承载力受人口密度、气候条件、灌溉技术和产业结构等众多因素共同影响[30]。与基准年相比,人均水资源生态足迹升高的城市包括新乡、淄博、东营和滨州,增幅分别为3.56%,1.90%,33.46%和12.99%;其余城市不同程度降低,郑州降幅最高达27.69%。人均生态赤字呈增长态势的有新乡、东营、菏泽和滨州,增幅分别为9.36%,11.57%,29.44%和8.44%;其他城市不同幅度下降,郑州和济宁降幅较大,分别为25.15%和23.65%。

|
图 3 2007—2020年黄河下游水资源状况空间分布特征 Figure 3 Spatial distribution characteristics of water resources in the lower reaches of the Yellow River basin from 2007 to 2020 |
各城市人均水资源生态足迹强度分布见图 3c,现状年间,人均水资源生态足迹强度较高的城市包括焦作、聊城、开封、滨州和菏泽,上述城市的水资源利用效率均有待提升;人均水资源生态足迹强度较低的城市具有经济发达、工业化程度高的特点,如郑州、济南和淄博等。相比于基准年,各城市人均水资源生态足迹强度均显著降低,尤以开封、郑州两市降幅最高。
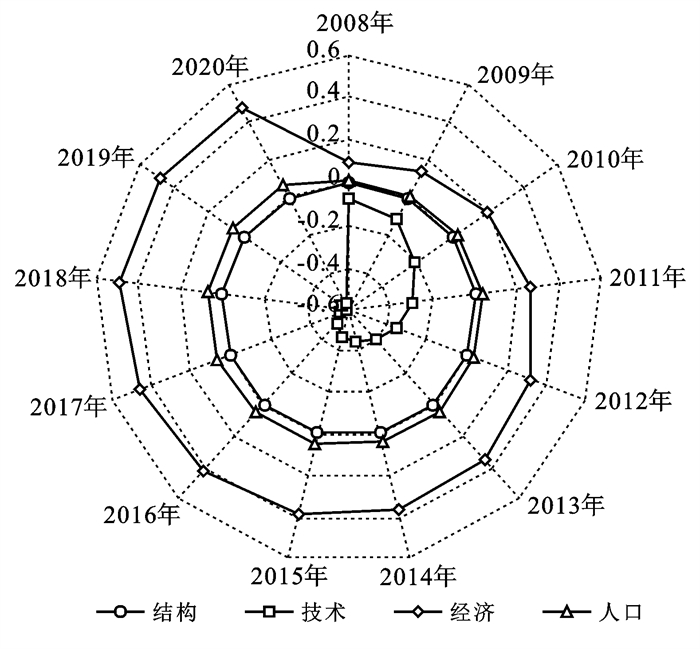
2.3 黄河下游水资源生态足迹驱动效应通过公式(5)—(10)对2007—2020年黄河下游水资源生态足迹驱动要素进行分解,结果如图 4所示。人口效应和结构效应的数值较小,两者对人均水资源生态足迹变化的驱动影响较弱,其中人口效应起弱正向效应,结构效应起弱负向效应。经济效应和技术效应是人均水资源生态足迹变化的主导因素,其中经济效应起到正向主导作用,水资源是经济发展的基础物质资料[31],黄河下游的经济增长过程使得水资源消耗量随之增加,导致人均水资源生态足迹升高;技术效应则起到负向主导作用,是黄河下游2007—2020年人均水资源生态足迹呈下降趋势的根本原因,工农业节水技术发展、高耗水产业转型等可有效提高用水效率,保障区域水资源的可持续利用。
|
图 4 2008—2020年黄河下游人均水资源生态足迹驱动要素 Figure 4 Driving factors of the per capita ecological footprint of water resources in the lower reaches of the Yellow River basin from 2008 to 2020 |
由公式(11)—(21)对黄河下游人均水资源生态足迹和生态赤字进行预测,经后验差检验,两者预测精度均满足合格以上的精度要求。预测结果表明(图 5),黄河下游2021—2030年人均水资源生态足迹和生态赤字维持下降趋势,其中人均水资源生态足迹由0.444 hm2/人降至0.404 hm2/人,降幅为9.01%;人均水资源生态赤字由0.387 hm2/人降至0.359 hm2/人,降幅为7.12%。虽然水资源生态压力有一定幅度的缓解,但由于生态赤字基数较大,水资源可持续利用形势依旧十分严峻,如何有效缓解黄河下游水资源生态压力是目前亟待解决的问题。

|
图 5 黄河下游2021—2030年水资源状况预测 Figure 5 Prediction of water resources in the lower reaches of the Yellow River basin from 2021 to 2030 |
运用生态足迹理论对2007—2020年黄河下游水资源生态足迹时空分布特征的分析结果表明,黄河下游水资源生态足迹远超生态承载力,区域水资源生态赤字状况严重;水资源生态足迹与生态赤字年际间均呈波动降低的趋势,用水效率逐渐提高,其中农业用水是最大的水资源生态足迹账户,比例达67.29%;黄河三角洲是黄河下游水资源生态压力最大区域,该区域水资源可持续利用状况最差,淄博、济南、郑州和泰安生态压力相对较小。
基于LMDI模型的水资源生态足迹驱动要素分解结果表明,经济效应和技术效应是2007—2020年黄河下游水资源生态足迹变化的主导因素,其中经济效应起正向主导作用,技术效应起负向主导作用。
通过灰色预测模型GM(1, 1)的水资源生态足迹预测结果表明,2021—2030年黄河下游水资源生态足迹和生态赤字虽有一定幅度的降低,但由于生态赤字基数较大,未来水资源可持续利用形势依旧十分严峻。
| [1] |
徐珊, 夏丽华, 陈智斌, 等. 基于生态足迹法的广东省水资源可持续利用分析[J]. 南水北调与水利科技, 2013, 11(5): 11-15. |
| [2] |
赵自阳, 李王成. 基于生态足迹的河南省水资源评价分析[J]. 节水灌溉, 2016(12): 80-84. |
| [3] |
汪伦焰, 黄昕, 李慧敏. 基于CW-FSPA的黄河流域九省水资源承载力评价研究[J]. 中国农村水利水电, 2021(9): 67-75. |
| [4] |
刘丽颖, 官冬杰, 杨清伟, 等. 基于人工神经网络的喀斯特地区水资源安全评价[J]. 水土保持通报, 2017, 37(2): 207-214. |
| [5] |
李新, 石建屏, 曹洪. 基于指标体系和层次分析法的洱海流域水环境承载力动态研究[J]. 环境科学学报, 2011, 31(6): 1338-1344. |
| [6] |
李菲, 张小平. 甘肃省水资源生态足迹和生态承载力时空特征[J]. 干旱区地理, 2020, 43(6): 1486-1495. |
| [7] |
Rees W E. Revisiting carrying capacity: Area-based indicators of sustainability[J]. Population and Environment, 1996, 17(3): 195-215. DOI:10.1007/BF02208489 |
| [8] |
岳晨, 刘峰, 杨柳, 等. 北京市2010-2019年水资源生态足迹和生态承载力[J]. 水土保持通报, 2021, 41(3): 291-295. |
| [9] |
徐中民, 张志强, 程国栋. 甘肃省1998年生态足迹计算与分析[J]. 地理学报, 2000, 55(5): 607-616. |
| [10] |
黄佳, 徐晨光, 满洲. 基于生态足迹的山东省水资源承载力研究[J]. 人民长江, 2019, 50(2): 115-121. |
| [11] |
黄林楠, 张伟新, 姜翠玲, 等. 水资源生态足迹计算方法[J]. 生态学报, 2008, 28(3): 1279-1286. |
| [12] |
杜轶, 郭青霞, 张勇. 2种不同算法的水资源生态足迹动态比较分析: 以山西省为例[J]. 水土保持学报, 2021, 35(4): 165-171. |
| [13] |
马剑锋, 秦腾, 佟金萍. 干旱区水资源生态足迹变动及影响因素的分析[J]. 统计与决策, 2016(18): 100-103. |
| [14] |
金昌盛, 邓仁健, 刘俞希, 等. 长江经济带水资源生态足迹时空分析及预测[J]. 水资源与水工程学报, 2018, 29(4): 59-66. |
| [15] |
赵金辉, 连兴容, 陈欣怡, 等. 匹配黄河流域高质量发展的工业布局模式研究[J]. 人民黄河, 2021, 43(4): 18-23. |
| [16] |
张金萍, 肖宏林. 黄河流域灌区农业用水研究发展历程与展望[J]. 灌溉排水学报, 2020, 39(10): 9-17. |
| [17] |
董战峰, 璩爱玉, 冀云卿. 高质量发展战略下黄河下游生态环境保护[J]. 科技导报, 2020, 38(14): 109-115. |
| [18] |
刘建华, 黄亮朝. 黄河下游水资源利用与高质量发展关联评估[J]. 水资源保护, 2020, 36(5): 24-30. |
| [19] |
王慧亮, 李卓成. 基于能值水生态足迹模型的黄河流域水资源利用评价[J]. 水资源保护, 2022, 38(1): 147-152. |
| [20] |
陈丽, 周宏. 基于模糊综合评价和主成分分析法的岩溶流域水资源承载力评价[J]. 安全与环境工程, 2021, 28(6): 159-173. |
| [21] |
路瑞, 赵琰鑫. 基于水资源生态足迹的黄河流域水资源利用评价[J]. 人民黄河, 2020, 42(11): 48-52. |
| [22] |
左其亭, 姜龙, 冯亚坤, 等. 黄河沿线省区水资源生态足迹时空特征分析[J]. 灌溉排水学报, 2020, 39(10): 1-8. |
| [23] |
卢亚丽, 徐帅帅, 司保江, 等. 黄河流域九省(区)水资源环境承载力动态演变特征研究[J]. 人民黄河, 2021, 43(11): 103-108. |
| [24] |
涂正革, 谌仁俊. 工业化、城镇化的动态边际碳排放量研究: 基于LMDI"两层完全分解法"的分析框架[J]. 中国工业经济, 2013(9): 31-43. |
| [25] |
马景, 武周虎, 邹艳均, 等. 基于灰色马尔科夫模型的南四湖水质预测[J]. 水资源保护, 2021, 37(5): 153-158. |
| [26] |
康春涛, 贡力, 王忠慧, 等. 利用灰色残差GM(1, 1)-Markov模型预测水工混凝土的劣化[J]. 水利水运工程学报, 2021(1): 95-103. |
| [27] |
李志超, 刘升. 基于ARIMA模型、灰色模型和回归模型的预测比较[J]. 统计与决策, 2019, 35(23): 38-41. |
| [28] |
段文婷, 陈有川, 张洋华, 等. 黄河下游地区农村居民点数量变化的时空特征及其影响因素研究[J]. 城市发展研究, 2021, 28(6): 19-24. |
| [29] |
燕永芳. 黄河下游两岸沿线城市水-能源-粮食耦合系统协调性研究[D]. 河南郑州: 华北水利水电大学, 2021.
|
| [30] |
雷亚君, 张永福, 张敏惠, 等. 新疆水资源生态足迹核算与预测[J]. 干旱地区农业研究, 2017, 35(5): 142-150. |
| [31] |
周召红, 吴江. 县域经济社会发展与水资源时空差异关系分析: 以宜昌市为例[J]. 人民长江, 2021, 52(9): 101-106. |
 2023, Vol. 43
2023, Vol. 43 

