2. 深圳中广核工程设计有限公司, 广东 深圳 518000
2. China Nuclear Power Engineering Co. Ltd., Shenzhen, Guangdong 518000, China
土壤水分入渗是地面水、土壤水及地下水互相转化的重要环节,是研究水文地质条件基本要素之一[1]。伴随着国家战略规划中低放射性废物地质处置、地下油库封存、水利水电工程等地下能源环境工程逐步实施,工程场地水文地质条件的适宜性已经成为评价地下工程最终性能的关键指标之一。因此,研究基岩表层风化层渗透特性,提出其渗透系数确定方法,对地下工程最终性能评价具有重要的工程应用价值。土壤渗透系数是评价土壤入渗性能的关键参数。为了准确获取该参数,现阶段常采用现场试验方式测定这一关键参数。为此,国内外学者提出并设计了不同类型的试验方法与仪器,用于提高测量结果精度,常见方法包括渗坑法、双环法、Guelph入渗仪法、张力入渗仪法等。张力入渗仪最早由Perroux和White(1988)共同设计[2],采用正、负水头方式测定土壤水分入渗过程,具有测量精度高、野外耗水少、轻便等优点,并且可实时自动采集数据,能够适应各种复杂的地质环境[3-4]。现阶段,在张力入渗仪测定土壤水力特性方面国内学者已经开展了较为系统的研究。研究重点包括不同土地利用方式和不同植被类型的入渗研究、有机质土壤吸渗特性研究、滨海地区盐渍土入渗特性研究等。总体而言,土壤渗透系数受土壤质地、土地利用情况、孔隙度、初始含水量等因素的影响[5-7]。通常情况下,土壤中砂砾含量越多、黏粒含量越低,土壤渗透系数越大[8]。同时,土壤渗透系数随不同土地利用类型的深度变化情况也有所不同[9]。表层土壤是否经过处理、是否有无机质的累积、土壤的盐分类型也会对土壤入渗性能的评价产生影响[10-11]。目前,土壤渗透参数计算方法主要有稳态方法、瞬态方法和反推参数法[12]。稳态方法假设土壤各向同性、均质且具有均一的含水量,采用Wooding公式进行求解[13]。在此基础上,又进一步发展并提出了4种计算渗透系数的方法,即非线性回归法[14]、多压力方法[15]、White-Sully方法(简称WS方法)[16]和多盘径方法[17]。为了解决低渗透黏土试验过程中所需时间较长这一难题,部分学者推导出相对更为灵活的瞬态方法进行数据分析,包括单盘单次测定法[18]、多盘径方法[19]和多吸渗率法等。然而,由于现场试验过程的复杂性,实际利用Richards方程数值解的反推参数法来计算土壤渗透参数的研究甚少[12]。综上所述,现阶段入渗试验相关研究对象多以第四系松散土层为主,而花岗岩地区基岩风化层的应用案例甚少,且关于不同方法在基岩地区地表风化层的研究尚未见报道。基于此,本文以中国南部滨海工程场地花岗岩风化层为研究对象,采用张力入渗仪开展不同土壤类型及地貌的渗透特性试验研究。对不同方法计算的结果进行对比分析,并基于地质统计学方法刻画场址内表层风化层渗透系数空间分布特征,探讨不同计算方法在基岩风化层适用性,为研究区工程场地的最终安全性能评价提供基础数据,亦对类似地区渗透特性研究具有一定的借鉴意义。
1 研究区概况 1.1 自然地理研究区位于中国南部滨海地区,属亚热带海洋性气候,雨量充沛,气候温和。多年平均气温为22.3 ℃,多年平均年降水量约为2 348 mm,年平均湿度82%。研究区所在山体呈北东东走向,高程一般170.0~265.5 m。山体南部临南海海域,受台风、地表水流侵蚀及物理风化作用明显,地形较陡峻。北侧坡度较缓,北侧沟谷存在常年地表径流的溪水,径流量随季节降雨波动较为明显。
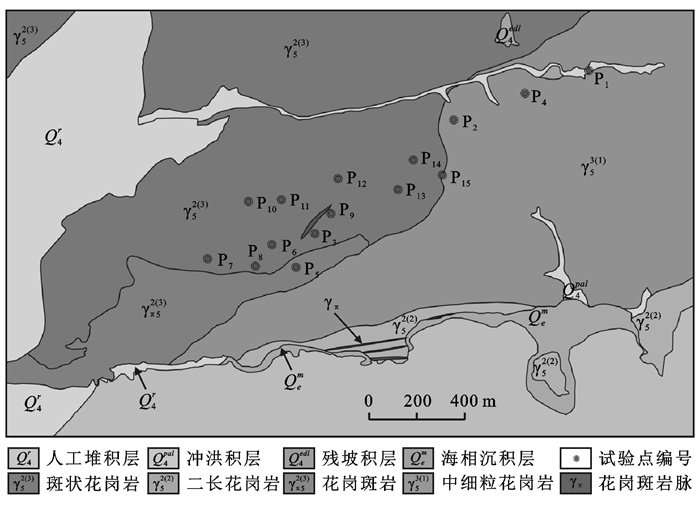
1.2 地质、水文地质概况研究区以丘陵地貌为主,地层和岩性较为单一。基岩主要由燕山期侵入的花岗岩为主,第四系覆盖层主要由冲洪积物的砂层与砾石层、残坡积物砾质黏性土及海相砂质黏性土组成。花岗岩按照侵入时代由老到新可分为:粗粒二长花岗岩、斑状花岗岩、中—细粒花岗岩和花岗斑岩(图 1)。其中侵入的岩脉包括花岗斑岩脉、闪长玢岩脉、伟晶岩脉。由于地处湿热气候带,花岗岩体之上普遍发育硅铝黏土型风化壳。研究区地下水类型主要包含松散岩类孔隙水和基岩裂隙水。场地水文地质结构可分为浅部的孔隙—裂隙网络结构与中下部的裂隙网络结构,岩脉发育地段为脉状结构。地下水补给主要以大气降水的垂直入渗为主,少数通过山体西北侧侧向径流补给。多数地下水从上向下运移排泄到场地山体北侧沟谷与南侧海域,少数以下降泉的形式出露。
|
图 1 研究区地质结构与试验点位置 |
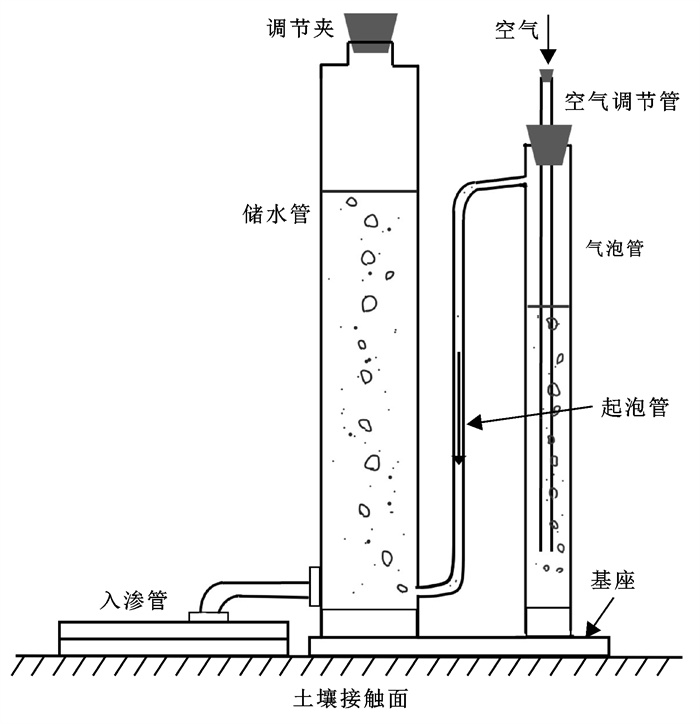
本次试验采用的是法国生产的型号为SW080 B张力入渗仪[20-21],设备主要由气泡管、储水管、入渗盘、起泡管及连接软管等组成(图 2)。在一定的水压条件下水分通过入渗圆盘向土壤缓慢入渗,通过设置不同的压力水头,测量相应水分的入渗速率,以此估算土壤的渗透系数及吸渗率等参数。
|
图 2 张力入渗仪示意图 |
考虑到研究区基岩风化层质地较为均匀、含水量差异较小,本研究采用单盘方式开展入渗试验研究。数据解译分别选择了稳态方法中的非线性回归方法、多压力方法和WS方法及瞬态方法中的单盘单次方法进行分析,各个方法的基本原理如下:
(1) 非线性回归法(NR)[14]是在Wooding方法和Gardner方法[22]的基础上推导出不同负压条件下土壤非饱和渗透系数表达式:
| $ Q=\pi r^2 K_{s a t} \exp (a h)\left(1+\frac{4}{\pi r a}\right) $ | (1) |
式中:Q为稳定入渗量(L3/T); r为圆盘半径(L); K(h)为与负压h对应的稳定入渗率(L/T); a为经验系数(L-1), 表示土壤孔隙的分布特征; Ksat为饱和渗透系数(L/T)。
(2) WS方法[16]是基于Wooding方法进一步考虑土壤基质势通量这一因素,推导出土壤渗透系数K数学方程:
| $ K=\frac{Q}{\pi r^2}-\frac{4 b S^2}{\left(\theta_0-\theta_i\right) \pi r} $ | (2) |
式中:b为形状系数, 一般取值为0.55; S为土壤的吸渗率(L/T0.5); θ0,θi分别表示初始与最终的土壤体积含水量(L3/L3)。
(3) 多压力方法(MP)[15]是通过测量两个相邻段的压力和稳定入渗率来计算相应的渗透系数K:
| $ \begin{gathered} K_{i+1 / 2}=\exp \left(\frac{\ln q_i+\ln q_{i+1}}{2}\right) /\left(1+\frac{4}{\pi r} \frac{h_i-h_{i+1}}{\ln \left(q_i / q_{i+1}\right)}\right) \\ (i=1, 2, \cdots, n-1) \end{gathered} $ | (3) |
式中:qi, hi为第i段单位土壤稳定入渗率(L/T)与负压(L); Ki+1/2为相邻两段平均土壤渗透系数。
(4) 瞬态方法[18]中的单盘测定法是基于一维入渗理论[23]提出土壤渗透系数K的计算方法:
| $ K=\frac{3}{2-b}\left[C_2-\frac{\gamma C_1^2}{r\left(\theta_0-\theta_i\right)}\right] $ | (4) |
| $ \frac{d I}{d \sqrt{t}}=C_1+2 C_2 \sqrt{t} $ | (5) |
式中:t为入渗时间(T); γ为忽略了重力影响的理论常数, 一般取值在0.6~0.8之间; C1, C2为dI/dt与t图形线性拟合线的参数(L/T0.5); I为累积入渗深度(L)。
2.2 研究方法为了查明地表基岩风化层入渗特征,本文分别选择研究区不同的地貌与岩性单元,于2020年10月27—29日,共计开展了15组土壤入渗试验,试验点位置如图 1所示。试验具体过程如下:首先除去地表植被和石块,整理出直径约40 cm的平整地面,并铺上厚度约2~3 cm的细砂。仪器加水,将盘中的空气全部排出,检查气密性。向气泡管中注水后盖上盖子,稍松开顶部螺帽并调整空气调节管底端位置,调节张力。再将浸泡在水中的入渗盘连接到仪器软管上,轻微晃动仪器与入渗盘,使仪器内部气泡排空,并将仪器小心放在测定点上,使其与细砂紧密接触。最后将电子采集器数据采集间隔设置为1 s,记录每秒储水管的水面位置。每组试验均从较高的张力测量值开始,依次降低。由于各个试验点的位置和土壤情况不同,每组入渗试验初始设置的负压水头值不同。为了研究该区域基岩风化层土壤饱和过程,首先选取相同张力条件下的不同试验点,绘制入渗量随时间的变化曲线图,对累积入渗量的变化过程进行分析。采用不同计算方法获取风化层渗透系数,根据研究区地貌及土壤特征进行分类,对比与分析不同特征类别土壤渗透系数产生差异的可能原因。最后,采用简单克里金插值方法进行空间统计分析,结合研究区地质与水文地质特征,综合分析区内地表风化层渗透系数的空间分布特征,最终为工程场地的性能评价提供基础数据。
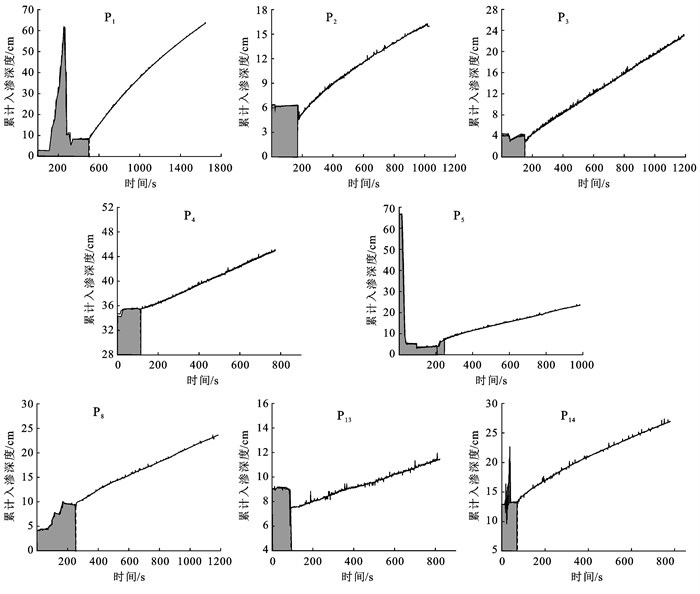
3 结果与分析选择负压水头为10 cm的情况下,部分试验点的累积入渗深度I随时间t的变化过程曲线如图 3所示。由图 3可知,大部分试验点的累计入渗深度在试验开始后的200 s左右后不再波动,随时间呈线性增长的趋势,即认为土壤表层风化层入渗率接近稳定状态。其中,P1试验点在试验开始后有较明显的大范围波动,且需要更长的时间达到饱和,其原因主要是由于开始阶段进行试验调试导致的。其余试验点的波动幅度较小。每组试验入渗速率接近稳定状态的测试时间约为1 000 s
|
图 3 部分试验点入渗量随时间变化曲线 |
选取各试验点稳定状态下的试验数据,用不同方法计算各负压水头条件下的渗透系数,每种方法取平均值作为此试验点的渗透系数,结果详见表 1。从数据计算结果可知,不同方法计算的渗透系数存在一定差异。其中,试验点P1的偏差最大,试验点P4,P6,P7,P12,P13及P14的各方法所得结果较为接近。对大多数试验点,非线性回归法和多压力方法的计算值较为接近,而WS方法相较于其他稳态方法而言结果偏大,瞬态方法的计算结果普遍小于稳态方法,所有方法的计算结果均在经验值的参考范围内。
|
|
表 1 各试验点平均渗透系数统计结果 |
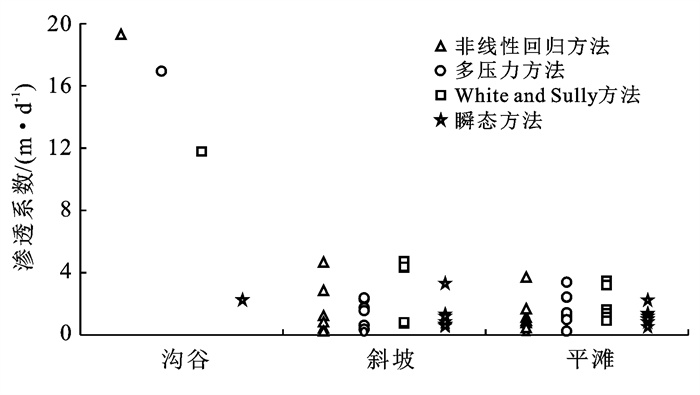
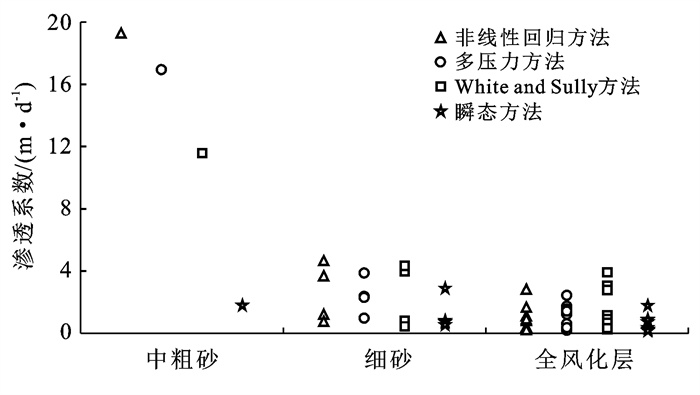
根据不同的地貌特征与土壤质地,将各方法计算出的渗透系数进行对比分析。不同地貌单元的渗透系数如图 4所示。结果表明,从地貌特征来看,研究区沟谷获得的渗透系数要明显大于斜坡和平滩地区,计算结果分布在3.627~19.221 m/d之间,这是由于受常年溪水冲刷作用,水流作用较强,且颗粒直径较为均匀且直径相对较大,渗透能力相对较强。斜坡地区的渗透系数分布在0.036~4.592 m/d之间,平滩地区的则分布在0.023~3.879 m/d之间,略小于前者,两者渗透性差异不明显。这可能是因为对于斜坡与平滩地区,地势相对较为平坦,水流作用较弱,沉积以较细颗粒的细砂与黏土为主,渗透系数相对较小。同时,对于沟谷地区,非线性回归方法的计算结果普遍偏大,瞬态方法的计算结果明显小于稳态方法;对于斜坡地区,非线性回归方法和WS方法的计算结果较为接近,多压力方法和瞬态方法的计算结果较为接近;对于平滩地区,3种稳态方法的计算结果较为接近,瞬态方法的计算结果偏小。不同土壤质地的渗透系数如图 5所示。从土壤质地来看,细砂的渗透系数分布在0.435~4.334 m/d之间,全风化层的渗透系数分布在0.023~3. 918 m/d之间,细砂的渗透能力与全风化层地区总体上相差不大,各方法计算结果的差异性不明显。全风化层的土壤主要以黏土矿物为主,如高岭石、蒙脱石等,形成了典型的硅铝黏土型风化壳,颗粒较小,渗透能力弱,这是导致其渗透性相对较差原因。中粗砂的渗透系数分布在1.787~19.221 m/d之间,主要分布在沟谷与斜坡地区,土壤粒径较大,渗透能力普遍较强,但不同计算方法的结果差异较大。相对而言,稳态方法中的非线性回归方法计算的渗透系数偏大,而瞬态方法计算值相对偏小。
|
图 4 不同地貌特征土壤平均渗透系数 |
|
图 5 不同土壤质地平均渗透系数 |
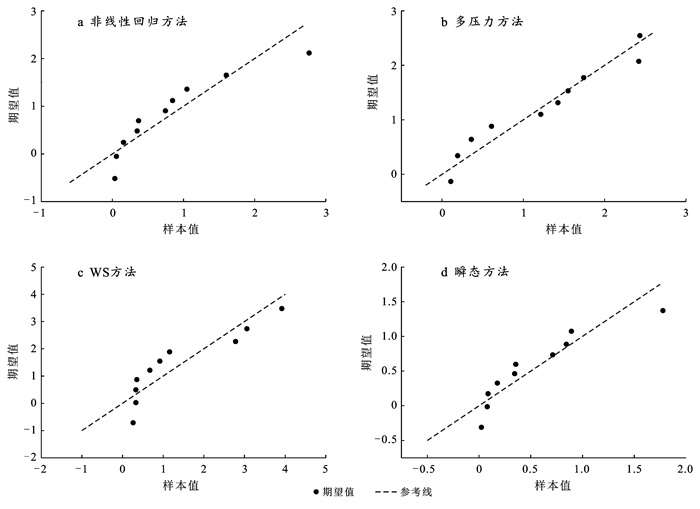
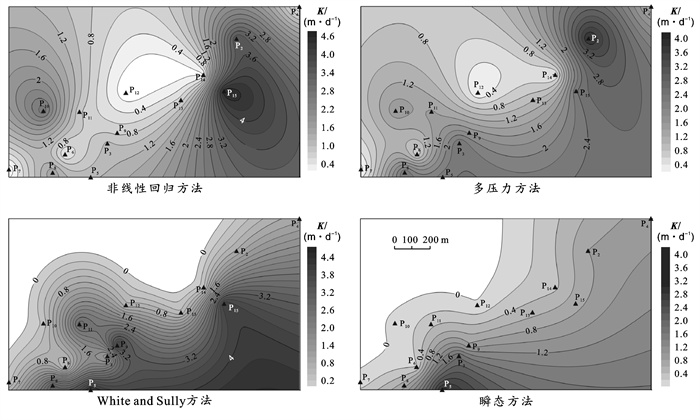
考虑到研究区基岩风化层岩性较为单一,空间差异性较小,可采用地质统计插值方法描述渗透系数在空间上的分布特征。试验点P1位于研究区山体北侧的沟谷地区,地貌类型与其他试验点不同,所求得的渗透系数值也显著高于其他试验点,为避免空间插值时出现“孔洞”效应,故本次插值时将该点去除。利用Q-Q图判断渗透系数计算结果是否满足正态分析(图 6),同时采用K-S检验方法对全风化层地区数据进行显著性检验。结果表明非线性回归法的显著性p值为0.843,多压力方法为1.000,WS方法为0.415,瞬态方法为0.629,均大于0.05,无显著性差异,满足正态分布。据此,采用简单克里金插值方法对各数据计算方法获得的渗透系数进行空间统计分析,结果如图 7所示。研究区内的渗透系数呈明显南高北低的趋势。结合研究区地形可知,地形较高一侧基岩风化层渗透能力普遍较强,地形较低处风化层的渗透能力相对较弱。稳态方法中的非线性回归方法和多压力方法的插值结果较为接近,东部存在渗透系数较高的区域,西部的渗透系数相对较低。稳态方法中的WS方法和瞬态方法的插值结果较为相似,南部和东部的区域渗透系数较高,而东部和北部由于无实测数据,在图中显示为空白。总体而言,研究山体地形较高较陡处渗透系数最高,地势较缓处存在明显渗透系数较低的区域,这可能与山体的风化程度、沉积的地层岩性有关,地形较高位置沉积颗粒较粗,渗透能力也相对较强,地势较缓处水动力较弱,沉积颗粒较细,渗透能力相对较弱。
|
图 6 各方法渗透系数结果Q-Q图 |
|
图 7 基岩风化层渗透系数空间分布图 |
试验结果表明张力入渗仪在本研究的基岩地区具有较好的适用性,不同方法计算的渗透系数存在一定差异。总体而言,稳态方法中的WS方法的计算结果数值偏大,瞬态方法的结果相对偏小。基于克里金空间插值结果整体上分为两类,非线性回归法、多压力法两者数据计算结果数值较为接近,获得的基岩风化层渗透系数的空间分布特征相似。而WS方法和瞬态方法计算的渗透系数及其空间分布特征较为相似。其原因可能是由于WS方法和瞬态方法的计算结果除了受入渗速率的影响之外,还受到初始含水量与最终含水量的影响。而目前测量最终含水量是相对困难的,本文中这两个参数均采用经验值,故使得数据计算结果与其他两种方法存在一定的误差。石长春等总结国内外的相关入渗试验研究,认为在土壤剖面较为均匀、含水量差异较小时,可以选择稳态方法,而试验时间有限时,可以应用瞬态方法,无时间限制时,可以采用稳态方法和瞬态方法[24]。对于本研究区基岩风化层而言,多数点位的入渗试验能够较快达到稳定状态,数据采用自动采集方式,精度较高,能够同时满足稳态计算方法和瞬态计算方法的需求。其次,WS方法和瞬态方法受到初始含水量与最终含水量参数的影响,计算结果的不确定性较大。根据不同计算方法的平均值可知,多压力方法的计算结果更接近平均值,参数相对较少,结果不确定性也相对较小。基于此,可以认为稳态方法中的多压力方法相对更适用本研究区的基岩风化层。
不同的地貌单元及土壤质地也会影响渗透系数,尤其是沟谷和斜坡中的中粗砂对渗透系数的作用较为明显,全风化层的斜坡和平滩地区渗透系数存在差异,但并不明显。显然,粒径大的土壤渗透能力强,粒径小的土壤渗透能力弱[9-10]。结合研究区的地形及地质概况,研究区地形较高位置山脊处,沉积颗粒较粗,渗透能力较强。而在地形较低位置,土壤颗粒较细,渗透能力相对较弱。这与前人得到的结论相符[25-26]。但是,在用WS方法和瞬态方法的结果进行空间插值时,出现了北部的渗透系数插值为负数的情况,这可能与插值参数的选取相关。
此次试验中还存在一些不足之处需要进一步分析和改进。在进行张力入渗试验时,由于试验点土壤表面不平整,需要在地表铺设一层细砂,以保证入渗盘面与土壤表面紧密接触,铺设的细砂会对试验结果造成一定影响。根据仪器的使用说明及相关参考文献,试验中所选用的砂层的渗透系数均大于所测土壤的,并在测定时在地表铺设一层与盘面孔隙大小相同的尼龙布,防止沙子进入土壤的大孔隙中,以此降低细砂和侧向渗透对渗透系数的影响。由于此次入渗试验的时间和经费有限,试验点数量偏少,不同特征的试验点个数较少,统计的结果存在偏差。在后续研究和工作中,可以增加室内的土壤测试和分析试验工作,例如增加土壤孔隙度的测定。在张力入渗仪测定的理论计算方法方面,各种方法的在不同土壤条件下的适用性以及方法之间的联系,还需进一步进行孔隙度以及含水量的测试,针对不同位置的土壤进行更准确地分析。
4.2 结论(1) 研究区基岩全风化层渗透系数分布在0.023~3.918 m/d,平均渗透系数约为0.971 m/d,与经验值相吻合。
(2) 研究区地形较高一侧基岩风化层渗透能力相对较强,地形较低处风化层的渗透能力较弱。
(3) 不同计算方法获得的渗透系数存在一定的差异性,且WS方法和瞬态方法计算结果受初始含水量与最终含水量影响明显,这是与非线性回归法、多压力法计算结果差异较大的主要原因。
(4) 稳态方法中的多压力方法更适用于研究区,可为类似地区基岩风化层渗透特性研究提供一定参考和借鉴。
| [1] |
邵明安, 王全九, 黄明斌. 土壤物理学[M]. 北京: 高等教育出版社, 2006.
|
| [2] |
Perroux K, White M I. Designs for disc permeameters[J]. Soil Science Society of America Journal, 1988, 52: 1205-1215. DOI:10.2136/sssaj1988.03615995005200050001x |
| [3] |
樊军, 王全九, 邵明安. 盘式吸渗仪测定土壤导水率的两种新方法[J]. 农业工程学报, 2007, 23(10): 14-18. |
| [4] |
朱良君, 张光辉, 任宗萍. 4种土壤入渗测定方法的比较[J]. 水土保持通报, 2012, 32(6): 163-167. |
| [5] |
林代杰, 郑子成, 张锡洲, 等. 不同土地利用方式下土壤入渗特征及其影响因素[J]. 水土保持学报, 2010, 24(1): 33-36. |
| [6] |
刘澄静, 角媛梅, 高璇, 等. 哈尼梯田水源区不同景观类型土壤水分的入渗特性及影响因子[J]. 水土保持通报, 2018, 38(3): 99-105, 111. |
| [7] |
黄金廷, 尹立河, 王晓勇, 等. 包气带垂向渗透系数的原位试验研究[J]. 水资源与水工程学报, 2013, 24(5): 33-35. |
| [8] |
刘目兴, 吴丹, 崔文虎. 长江三峡山地不同垂直带土壤入渗研究[J]. 水土保持学报, 2015, 29(3): 56-61. |
| [9] |
刘丽红, 蒋勇军, 王翱宇, 等. 岩溶槽谷区不同土地利用方式土壤入渗规律研究[J]. 水土保持通报, 2010, 30(4): 51-55, 59. |
| [10] |
王燕, 杨劲松, 王相平, 等. 滨海农田土壤入渗特性规律研究[J]. 灌溉排水学报, 2015, 34(8): 39-43. |
| [11] |
陈世平, 李毅, 付秋萍, 等. 不同含盐土壤圆盘入渗特征试验[J]. 农业工程学报, 2010, 26(4): 36-41. |
| [12] |
范军亮. 基于负水头的土壤水分运动特征研究及其参数推求[D]. 陕西杨凌: 西北农林科技大学, 2010.
|
| [13] |
Wooding R A. Steady infiltration from large shallow circular pond[J]. Water Resour Research, 1968, 4: 1259-1273. |
| [14] |
Logsdon S D, Jaynes D B. Methodology for determining hydraulic conductivity with tension infiltrometers[J]. Soil Science Society of America Journal, 1993, 57: 1426-1431. |
| [15] |
Ankeny M D, Ahmed M, Kaspar T C, et al. Simple field method determining unsaturated hydraulic conductivity[J]. Soil Science Society of America Journal, 1991, 55: 467-470. |
| [16] |
White I, Sully M J. Macroscopic and Research microscopic capillary length and time scales from field infiltration[J]. Water Resour Research, 1987, 23: 1514-1522. |
| [17] |
Scotter D R, Clothier B E, Harper E R. Measuring Saturated hydraulic conductivity and sorptivity using twin rings[J]. Australian Journal of Soil Research, 1982, 20: 295-304. |
| [18] |
Vandervaere J P, Vauclin M, Elrick D E. Transient flow from tension infiltrometers (I): The two-parameter equation[J]. Soil Sciencce Society of America Journal, 2000, 64: 1263-1272. |
| [19] |
Vandervaere J P, Vauclin M, Elrick D E. Transient flow from tension infiltrometers (Ⅱ): Four methods to determine sorptivity and conductivity[J]. Soil Science Society of America Journal, 2000, 64: 1272-1284. |
| [20] |
Ankeny M D, Kaspar T C, Horton R. Design for an automated infiltrometer[J]. Soil Science Society of America Journal, 1988, 52: 893-896. |
| [21] |
Minasny B, Alex B, McBratney A B. Estimation of sorptivity from disc-permeameter measurements[J]. Geoderma, 2000, 95: 305-324. |
| [22] |
Gardner W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Sciencce, 1958, 85: 228-232. |
| [23] |
Philip J R. Hillslo p infiltration divergent and convergent slops[J]. Water Resources Research, 1991, 27: 1035-1040. |
| [24] |
石长春, 樊军. 利用盘式吸渗仪确定土壤水力学参数研究进展[J]. 中国农学通报, 2017, 33(33): 127-134. |
| [25] |
李仁海, 周志超, 李杰彪, 等. 甘肃北山地区典型沟谷包气带土壤渗透特征研究[J]. 土壤通报, 2020, 51(6): 1380-1385. |
| [26] |
李杰彪, 苏锐, 周志超, 等. 高放废物处置库预选场址包气带土壤渗透性研究[J]. 土壤学报, 2015, 52(6): 1412-1421. |
 2022, Vol. 42
2022, Vol. 42 

