自然灾害威胁着人类的生存,同时加剧环境条件的恶化[1]。洪水灾害作为全球面临的十大自然灾害之一,每年造成的直接经济损失约占全球自然灾害总损失的20%[2],其中我国约有75%的国土面积存在洪水的隐患。随着强降雨天气引发的一系列洪涝灾害以及因洪涝灾害引起的次生地质灾害,给国家和人民造成了不可估量的人身及财产损失[3],2019年全国15省(自治区、直辖市)发生了108起造成人员死亡的山洪灾害事件,导致347人死亡[4]。
根据已有的数据资料快速推演、预估洪水灾害带来的影响,获取洪灾发生后洪水淹没范围以及洪水对蓄洪区流域桥梁、堤岸等建筑的影响资料,对防洪减灾具有重要意义。目前,对洪水演进进行模拟的方法主要有物理模型方法、水文模型法和水力学递推法。物理模型法主要通过简化地形、概化建筑物以及流态监测等研究洪水演进过程,董柏良等[5]建立了具有典型街区构造的洪水演进物理模型,定量分析了建筑物密度、绿化带设置等对洪水演进过程带来的影响,但是物理模型法有灵活性不高,受制于场地、经费等因素以及耗时长等缺点。在水文模型法中马斯京根法[6]的应用最为广泛,马斯京根法虽然能够模拟洪水在河流中的运动,并且易于稳定,步骤简单,但难以对地形相对复杂的河道进行分析。水力学递推法的核心是求解圣维南方程组,水力学模型目前主要可以分为3类,即一维水动力模型、二维水动力模型和三维水动力模型。一维水动力数值模型适用于对河段较长、河网简单的河流,苏飞等[7]通过建立一维河网水动力模型在洪水水流模型的基础上进行了枯水期水流运动模拟,模型能模拟出不同时期的水流运动,但对于面上水力要素计算精度有所缺乏。随着计算机技术的不断发展,三维水动力数值模拟逐步应用,李大鸣等[8]应用垂向坐标变换,结合水平有限元、垂向有限差分的分层方法建立了河道三维水流泥沙数学模型,对过流断面变化剧烈的河段提出了错层计算的方法。三维水动力模型相对于一维水动力模型和二维水动力模型有更高的精度,能反映垂向上水力要素的变化,但建模资料需求更为严格、全面且所耗时长会更高。水力递推法中平面二维水流数学模型以垂线平均的水流因素作为研究对象,能够很好地模拟计算平面流场及细部的变化情况,既能反映出水力因素在面上的分布及变化,又相对三维模型更为简便,目前应用广泛。其中,MIKE 21模型是水力递推法平面二维水动力学数值模拟软件,具有强大的前、后处理功能。在前处理方面,能根据地形资料进行网格的划分; 在后处理方面具有强大的分析功能。例如流场动态演示,计算特征点水位,实测与计算过程的验证,不同方案的比较等[9]。同时在蓄洪区水力递推法二维水动力模拟研究较少,本文以安徽省阜阳市阜南县濛洼蓄洪区的真实地形资料及淮河特大桥设计资料构建了基于MIKE 21非结构化网格的洪水演进影响模型,结合Global Mapper中地形分析模块生成糙率,并通过历史洪水过程对干湿水深等参数进行率定验证,采用纳什效率系数对模型进行控制,考虑桥梁建设后桥墩的阻水,并结合地形数据和数值计算结果对洪水演进过程中分洪历时、流速分布、水位变化等特征进行分析,旨在为濛洼蓄洪区防洪避灾、河道安全行洪及水量分配等提供一定的参考。
1 研究区概况濛洼蓄洪区是淮河流域于1953年设立的第一座行蓄洪区,位于安徽省西北部阜南县境内,处东经115°16′30″—115°57′18″,北纬32°24′19″—32°54′40″之间亚热带与暖温带的过渡带,属暖温带半湿润季风气候区,年平均气温15 ℃左右,年均降水量900 mm左右。濛洼蓄洪区处于淮河干流洪河口以下至南照集之间,南临淮河,北临濛河分洪道,汛期四面环水[10]。濛洼蓄洪区内地面高程一般为26.0~21.0 m,地势由西南向东北倾斜[11]。淮河特殊的地理条件,使得王家坝闸位于三河交界的扼襟控咽之处,而有了千里淮河“第一闸”的称号。王家坝闸也被誉为淮河防汛的“晴雨表”,是淮河灾情的“风向标”,同时习近平总书记也指出要把防汛抗洪工作作为重大任务,把确保人民群众生命安全放在首位。自1953年开始,仅有13个年份16次开闸蓄洪,最近一次开蓄洪时间是2020年7月。现状蓄洪区,设计蓄洪水位27.7 m,设计进洪流量1 626 m3/s,设计蓄洪库容7.50×108 m3[12]。
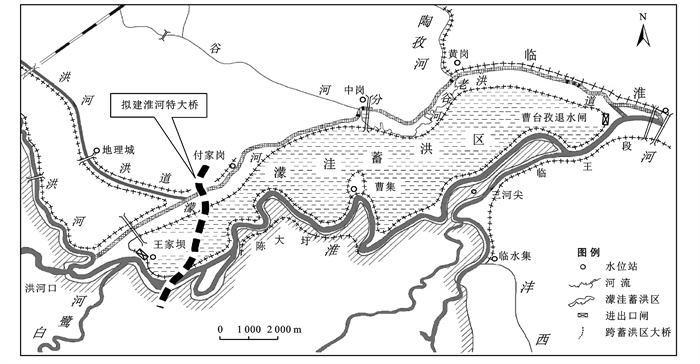
拟建王家坝特大桥(图 1)作为规划S238南延段的一段,是阜南县南北向中轴线的重要组成部分,也是阜阳市与河南固始县、淮滨县省际干线公路通道跨越淮河的控制性工程,拟建王家坝淮河特大桥全长12 680.5 m,设计主要控制点由北向南分别为濛左堤、濛河、濛洼蓄洪区北圈堤、王家坝保庄圩、濛洼蓄洪区南圈堤、淮河主河道,跨越淮河后进入河南境内。桥梁工程跨越淮河干流、濛洼蓄洪区和濛河分洪道及相应堤防,大桥桥墩和基础位于河滩地及堤脚附近,工程建设势必会对河势稳定、河道行洪、通航以及河道治理规划等产生一定的影响。
|
图 1 王家坝特大桥濛洼蓄洪区区域、桥梁位置、进出口闸门示意图 |
MIKE 21模型是研究地表水运动的二维数值模拟软件,运用在众多水动力模拟科研和工程实践中,模拟效果较好,对预测评价工作具有较大的指导性意义[13]。
MIKE 21水动力学基本方程如下[14]
平面二维水流的连续方程为:
| $ \frac{{\partial h}}{{\partial t}} + \frac{{\partial h\bar u}}{{\partial x}} + \frac{{h\bar v}}{{\partial y}} = hS $ | (1) |
式中: h为总水深, h=η+d, 其中d为静水深; η为河底高程; x, y为右手笛卡尔坐标系; S为点源流量; u, v分别为沿x, y坐标方向的平均流速。
平面二维水流动量方程:
| $ \begin{aligned} \frac{{\partial h\bar u}}{{\partial t}} + \frac{{\partial h{{\bar u}^2}}}{{\partial x}} + \frac{{\partial h\overline {uv} }}{{\partial y}} =& f\bar vh - gh\frac{{\partial \eta }}{{\partial x}} - \frac{h}{{{\rho _0}}}\frac{{\partial {P_a}}}{{\partial x}} - \frac{{\partial {h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial x}} + \frac{{{{\bar \tau }_{Sx}}}}{{{\rho _0}}} - \frac{{{{\bar \tau }_{bx}}}}{{{\rho _0}}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{xx}}}}{{\partial x}} + \frac{{\partial {s_{xy}}}}{{\partial y}}} \right) + \\ &\frac{{\partial \left( {h{T_{xx}}} \right)}}{{\partial x}} + \frac{{\partial \left( {h{T_{xy}}} \right)}}{{\partial y}} + h{u_s}S \end{aligned} $ | (2) |
式中: Pa为当地大气压强。
| $ \begin{aligned} \frac{\partial h \bar{v}}{\partial t}+\frac{\partial h \bar{v}^{2}}{\partial x}+\frac{\partial h \overline{u v}}{\partial y}=& f \bar{v} h-g h \frac{\partial \eta}{\partial y}-\frac{h}{\rho_{0}} \frac{\partial P_{a}}{\partial y}-\frac{\partial h^{2}}{2 \rho_{0}} \frac{\partial \rho}{\partial y}+\frac{\bar{\tau}_{S y}}{\rho_{0}}-\frac{\bar{\tau}_{b y}}{\rho_{0}}-\frac{1}{\rho_{0}}\left(\frac{\partial s_{y x}}{\partial x}+\frac{\partial s_{x y}}{\partial y}\right)+\\ & \frac{\partial\left(h T_{x y}\right)}{\partial x}+\frac{\partial\left(h T_{x y}\right)}{\partial y}+h v_{s} S \end{aligned} $ | (3) |
式中: u, v为x, y方向的流速分量; fu, fv为地球自转加速度; g为当地重力加速度; t为时间; ρ0为水的密度; Pa为当地大气压强; f=2ωsinφ Coriolis参量(其中ω为地球自转角速率; φ为地理纬度); Sxx, Sxy, Syx, Syy为4个辐射应力的分量; us,vs为源汇项水流的流速; τsx,τsy为风场摩擦力在x, y上的分量; τbx,τby为河床摩擦力在x, y方向上的分量; Txx, Txy, Tyx, Tyy为水平黏滞力。
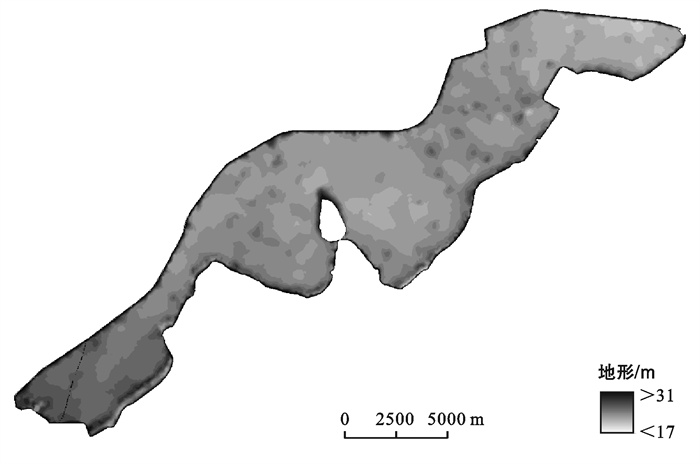
2.2 模拟范围模型计算范围为濛洼蓄洪区,蓄洪区以淮河左堤和濛河分洪道右堤,以及王家坝进洪闸和曹台孜退水闸构成蓄洪圈堤,总面积约为180.4 km2。自1953年濛洼蓄洪区建成运用至今,区内平面形态基本无变化,但王家坝河段中低水大断面处却有变化,主要体现在横向变形伴随着深泓下切,断面趋于窄深,高水两汊冲淤相加,大断面总体呈微冲趋势,进出水两闸门附近地形变化较大,故地形采用实测濛洼蓄洪区资料,计算区域、桥梁位置、进出口闸门如图 1所示,原始地形资料处理后得到的模拟范围地形如图 2所示。
|
图 2 濛洼蓄洪区洪水演进范围地形图 |
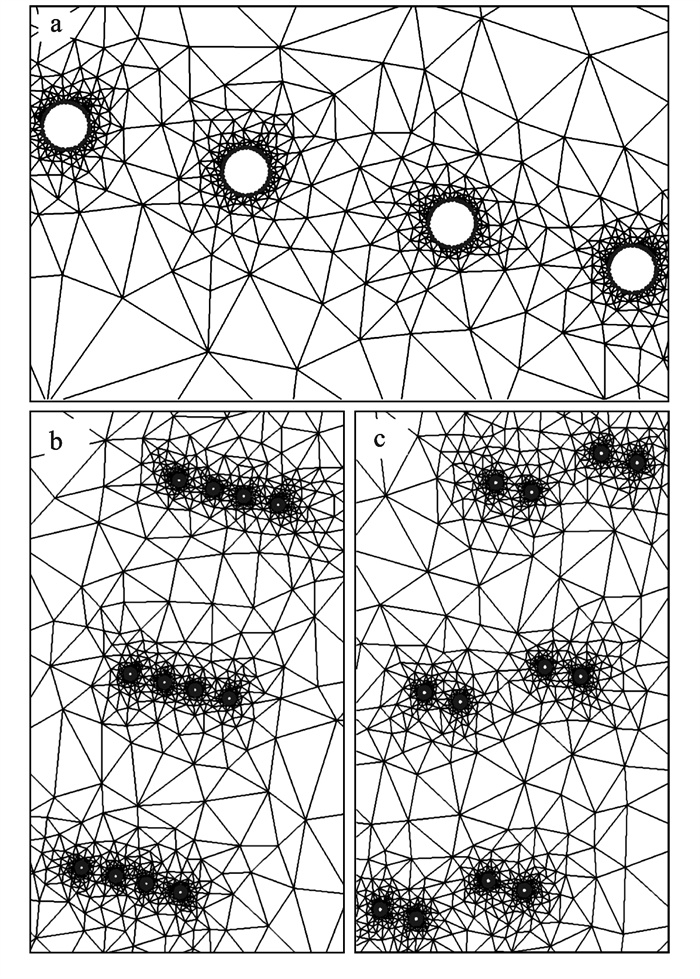
濛洼蓄洪区并非类长直河道,形状极不规则,采用非结构化网格进行计算,模型对庄台及王家坝特大桥桥墩等部位网格进行局部加密(图 3a),同时扣除王家坝等保庄圩的保护范围。共划分40 000个网格,布置110 278个节点,计算单元201 342个,为了反映桥墩处水力要素情况,扣除桥墩主体并加密桥墩节点个数。其中桥墩在长直桥梁段采用并排式(图 3b)设计,在弯道处桥墩交错(图 3c)减小水阻,桥墩局部网格如图 3所示。
|
图 3 濛洼蓄洪区桥墩局部网格加密计算模型示意图 |
根据模型网格大小、水深条件动态调整模型计算时间步长,使CFL(Courant-Friedrich Levy)数小于0.8,达到满足模型稳定的要求,模型计算时间步数10 000,时间步长60 s[15]。结合Global mapper软件生成糙率替代传统手动划分糙率,陆地边界选择垂向零流速边界(滑动边界),上游进口边界采用王家坝闸流量过程,下游出口边界采用曹台孜闸流量过程。
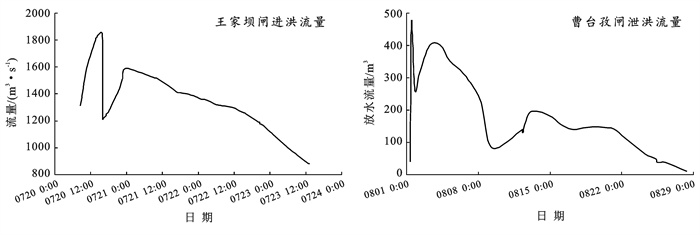
3 洪水演进模型验证本文采用纳什效率系数进行验证模型数据与最新实测数据的吻合度,且进洪过程与退洪过程衔接模拟避免分布模拟时水体分布变化的影响。选取距今最近一次蓄退洪过程即2020年7月20日08:00至8月28日08:00作为模型验证时段,模拟濛洼蓄洪区2020年一号洪水的进洪过程,上游边界条件采用2020年王家坝闸实测流量过程,下游边界曹台孜闸实测流量过程,2020年一号洪水开闸进洪流量1 310 m3/s,峰值流量达1 850 m3/s,历时约76.5 h,蓄洪总量3.75×108 m3,进、出口闸实测流量过程如图 4所示。
|
图 4 王家坝、曹台孜闸实测流量过程线 |
王家坝开闸进洪后,洪水到达曹台孜闸附近,大约需要2 d时间。通过曹集水位站对濛洼蓄洪区进洪前、洪水演进24 h时刻以及洪水演进48 h时刻水位验证,计算水位与实测水位吻合,模型纳什效率系数为0.93(图 5)。模型的模拟过程与实测成果吻合很好,建立的模型参数选择合理,能够较好地模拟濛洼蓄洪区内的洪水实时演进过程,可用于桥梁建设前后影响对比分析。

|
图 5 濛洼蓄洪区2020年洪水演进过程模拟结果 |
桥梁工程建设对蓄洪区洪水演进的影响主要体现在桥墩阻水延缓蓄洪区洪水进洪时间;桥梁前后水位变化使得流速分布变化;阻水建筑物直接导致桥前水位抬升。
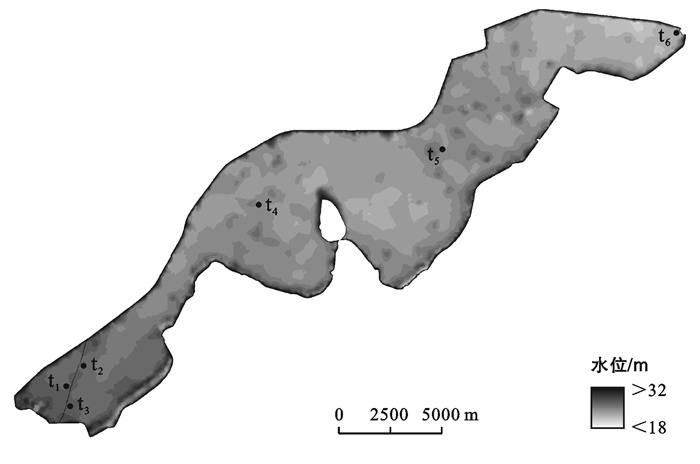
4.1 蓄洪区进洪时间特征分析为分析方便,本次主要对濛洼蓄洪区进洪过程进行模拟分析,初始条件为濛洼蓄洪区上边界王家坝闸开闸进洪,设计洪量为1 626 m3/s。选取工程位置附近特征点(t1,t2,t3)及濛洼蓄洪区内各特征点(t4,t5,t6),分析工程前后不同特征点处水位达到设计蓄洪水位所需的时间(图 6)。桥梁工程修建后,桥位附近特征点(t1,t2,t3)位置处较其他位置特征点分洪历史变化大,桥位附近t2特征点分洪历时比工程修建前滞后45 s(表 1)。
|
图 6 濛洼蓄洪区洪水演进历时特征点分布 |
|
|
表 1 工程前后洪水到濛洼蓄洪区各特征点时间 |
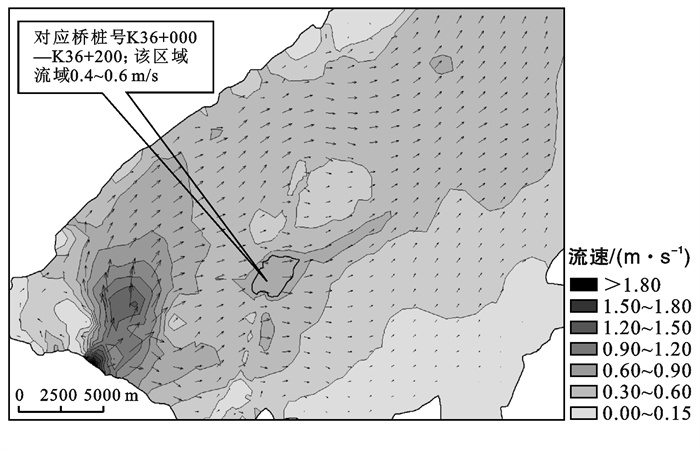
工程建设后区内进洪洪水演进计算结果表明,自王家坝闸开闸进洪开始,洪水到达曹台孜附近,大致需要2 d时间。洪水演进过程中,桥址断面的流速整体较小,约0.2~0.4 m/s;桥区范围的主流区宽度约200 m,对应线路桩号K36+000—K36+200范围,主流区流速值为0.4~0.6 m/s(图 7)。
|
图 7 濛洼蓄洪区洪水演进桥区附近流速分布(48 h) |
濛洼蓄洪区桥梁建成后,洪水的行洪受到桥墩影响,水流场在桥墩附近发生绕流,变化范围主要为桥墩局部,水流场整体流速较小,附近其他网格处的流速和流向并未发生变化。洪水演进96 h时,部分桥墩墩周流场分布局部放大情况如图 8所示。

|
图 8 蓄洪区洪水演进96 h墩周流场分布(局部) |
濛洼蓄洪区内流速会随着桥梁建设产生相应变化,蓄洪区分蓄洪阶段,区内流速整体受建桥影响较小,但对局部流速影响较大,流速峰值最大增幅为0.044 m/s,流速变化率最大7.409%。且工程前后各特征点的流速峰值差距很小,濛洼蓄洪区内工程前后特征点相应的流速峰值统计情况详见表 2。
|
|
表 2 濛洼蓄洪区各特征点流速峰值及出现时间比较 |
由于桥墩的阻壅作用,蓄洪区进退洪过程中,位于桥墩区域水流会有抬高或降低,导致蓄洪区内水位变化。
为了反映工程后蓄洪区内蓄水位的变化情况,选取具有代表性的特征点的水位过程进行分析。通过特征点处工程前后濛洼蓄洪区进洪过程的水位差值分析(分别选取蓄洪区洪水演进48 h,72 h及96 h时间点的工程前后水位差值),结果表明,不同洪水演进时间点,桥墩附近点位受到桥墩影响有所变化,进洪期间桥墩附近最大抬高值为0.006 m,水位最大变化率为-0.22‰。表 3反映了不同时刻蓄洪区内各点位处水位对比情况。
|
|
表 3 各时刻蓄洪区内各点位处水位对比情况 |
(1) 本文对濛洼蓄洪区建立了二维水动力模型,将蓄洪退洪过程作为整体统一进行数值模拟,验证结果显示模拟水位与历史水位纳什效率系数为0.93,模型设计合理,计算结果可靠,可用于桥梁建设工程水流数值模拟。
(2) 蓄洪区进退洪时,大桥附近主流区域分布在线路桩号K36+000—K36+200段,主流区流速值为0.4~0.6 m/s,其余部分流速较小。水流场在桥墩附近出现了明显的绕流,对桥墩附近流速场有影响;工程建成前后,通过特征点流速峰值对比分析,流速变化率最大为7.409%;进洪期间桥墩附近最大抬高值为0.006 m,水位变化率最大为-0.22‰;工程建成前后,洪水到达蓄洪区内各特征点的最大时间差为45 s。
(3) 本文以濛洼蓄洪区特大桥工程为例,模拟分析桥梁建设对蓄滞洪区洪水演进影响,模型能够较好地模拟蓄洪区内水力要素变化情况,且对于开展抗洪防涝工作及蓄洪区内工程建设具有较强的指导意义。然而MIKE 21二维水动力数值模拟对地形数据依赖性极强,以垂线平均值处理在深度方向的水力要素,也忽略了对流项的影响,在今后的研究中需要进一步的完善。
| [1] |
任伟义. 温州市洪涝台灾害应急管理能力提升研究[D]. 上海: 华东政法大学, 2015.
|
| [2] |
薛文宇. 城市暴雨积水及街道洪水模拟模型研究[D]. 天津: 天津大学, 2016.
|
| [3] |
刘恒洋. 基于DEM的洪湖分蓄洪区东块洪水淹没模拟研究[D]. 湖北武汉: 华中科技大学.
|
| [4] |
国家防汛抗旱总指挥部. 中国水旱灾害公报(2019)[M]. 北京: 中国水利水电出版社, 2021.
|
| [5] |
董柏良, 夏军强, 陈瑾晗. 典型街区洪水演进的概化水槽试验研究[J]. 水力发电学报, 2020, 39(7): 99-108. |
| [6] |
G Mccarthy. Unit Hydrograph and Flood Routing[C]//US: Conference of North Atlantic Division, 1939.
|
| [7] |
苏飞, 王士武, 陈雪, 等. 平原河网一维水流计算模型在洪水期和枯水期的应用[J]. 中国农村水利水电, 2008(1): 34-36, 39. |
| [8] |
李大鸣, 林毅, 周志华. 蓄滞洪区洪水演进一、二维数值仿真及其在洼淀联合调度中的应用[J]. 中国工程科学, 2010, 12(3): 82-89. |
| [9] |
许婷. 丹麦MIKE21模型概述及应用实例[J]. 水利科技与经济, 2010, 16(8): 867-869. DOI:10.3969/j.issn.1006-7175.2010.08.013 |
| [10] |
万长宇. 河道疏浚断面设计探讨: 以濛马河上段为例[J]. 工程与建设, 2019, 33(3): 373-375. DOI:10.3969/j.issn.1673-5781.2019.03.018 |
| [11] |
张红萍, 胡昌伟, 刘舒. 濛洼蓄滞洪区洪水淹没数值模拟[J]. 中国水利水电科学研究院学报, 2005, 3(4): 52-57. |
| [12] |
张鹏, 季益柱. 桥梁工程跨越蓄洪区对防洪的影响评价[J]. 治淮, 2018(4): 18-21. |
| [13] |
许婷. MIKE21 HD计算原理及应用实例[J]. 港工技术, 2010, 47(5): 1-5. |
| [14] |
班美娜, 武永新. 基于MIKE21 FM的南渡江河口段行洪能力分析[J]. 南水北调与水利科技, 2018, 16(2): 151-157. |
| [15] |
孙光春. 取排水口附近流场模拟及对通航的影响研究[D]. 辽宁大连: 大连海事大学, 2017.
|
 2022, Vol. 42
2022, Vol. 42 
